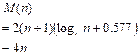Sorting
Sorting
is known as a fundamental operation in computer science. It is a task of
rearranging data in an order, such as, ascending, descending or lexicographic.
Data may be of any type like, numerical, alphabetical or string of alphanumeric.
Sorting also refers to rearranging a set of records based on their key values
when records are stored in a file.
It is well known that this task arises more frequently
in the world of data manipulation. From programming point of view the sorting
task is important for the following reasons.
- How to rearrange a
given set of data?
- Which data structures
are more suitable to store data prior to their sorting?
- How fast the sorting
can be achieved?
- How sorting can be
done in a memory constraint situation?
- How to sort various types
of data?
Several sorting techniques have been proposed to
address the above issues. In this chapter, the most important sorting techniques
are discussed. For each sorting technique the principal steps required to be
followed, timing analysis and possible way(s) of improving it and its applications
will be discussed. Finally, a comparison of all sorting techniques is provided.
BASIC TERMINOLOGIES
Throughout
the discussion of this chapter, some terms related to sorting will be referred.
These terms are defined in this section.
Internal sorting: When the set of data to be sorted is small enough
that the entire sorting can be performed in computer’s internal storage (primary
memory) then the sorting is called internal sort.
External sort: Sorting of a large set of data, which is stored in low
speed computer’s external memory (such as hard disk, magnetic tape etc.) is
called external sort.
Ascending order: An arrangement of data is called in ascending order
(also called increasing order) if it satisfies the “less than or equal to
(≤)” relation between any two data. In other words, if Ai and Aj are any two
data and Ai precedes Aj then Ai and Aj are said to be in ascending order if Ai
≤ Aj. If this
relation holds for any two data in the list then the list is sorted in
ascending order.
Example 14.1
Ascending order: [1, 2,
3, 4, 5,
6, 7, 8, 9]
Descending order: An arrangement of data is called in descending order (also
called decreasing order) if it satisfies “greater than or equal to (≥)” relation
between any two consecutive data. In other words, if Ai and Aj
are any two data and Ai precedes Aj then Ai and Aj are said to be in
descending order if Ai ≥ Aj.
If this relation holds for any two data in the list then the list is sorted in
descending order.
Example 14.2 Descending order: [9, 8,
7, 6, 5,
4, 3, 2, 1]
Lexicographic order: If the data are in the form of characters or string
of characters and they are arranged in the same order as in dictionary then it
is called lexicographic order.
Example 14.3 Lexicographic
order: [ada, bat , cat , mat,
max, may, min]
Collating sequence: This is an ordering for a
set of characters that determines whether a character is in higher, lower, or
same order compared to another. For example, the alphanumeric characters are
compared according to their ASCII code. Thus if we compare a (small letter) and A (capital
letter) then A comes before a, because ASCII codes of a and A are 96 and 65, respectively. A string of such characters are
ordered based on their constituent characters each comparing starting from the left
most character. In other words, Amazon
comes before amazing, Rama comes before Ramayan etc.
Examples 14.4 Collating
sequence: [AmaZon, amaZon, amazon, amazon1, amazon2]
Note: Collating sequence is same as
the lexicographic order except collating sequence considers string of any
characters including small and capital letters, digits, printable special symbols
etc. and sorted in an order based on their ASCII codes.
Random order: If the data in a list do not follow any ordering
mentioned above then we call the list is arranged in random order.
Examples 14.5 Random
order: [8, 6, 5, 9, 3, 1, 4, 7, 2]
[may, bat , ada, cat , mat, max, min]
Swap: Swap between two data storages implies the interchange of their contents.
Swap is also alternatively called interchange.
Example
14.6 Before
swap: A[1] = 11, A[5] = 99
After
swap: A[1] = 99, A[5] = 11
Stable sort: A list of unsorted data may contain two or more equal
data. If a sorting method maintains the same relative position of their
occurrences in the sorted list then it is called stable sort. A stable sort is
illustrated in Figure 14.1.

Fig. 14.1 Stable sort.
In place sort: Suppose, a set
of data to be sorted is stored in an array A.
If a sorting method takes place within the array A only, that is, without using any other extra storage space then
it is called an in place sorting method. In other words, in place sorting does
not require extra memory space other than the list itself and hence a memory
efficient method.
Item: An item is a data or element in the list to be sorted. An item may be
an integer value, string of characters (alphabetic or alphanumeric), a record
etc. An item is also alternatively termed as key, data, element etc.
Convention to be followed: In our subsequent discussions, we will follow the
following conventions, unless explicitly specified.
- A list implies an array
of elements.
- Type of the items to
be sorted is integer type.
- Range of index of an
array varies from 1 to N, where N is the size of the array.
- Sorting implies the
sorting of items in ascending order.
- An input list can be
obtained from the keyboard reading at a time or stored in a file.
SORTING TECHNIQUES
Many
sorting techniques have been developed so far. All sorting techniques can be
classified into two broad categories: internal sorting and external sorting. In
internal sorting, all items to be sorted are kept entirely in the computer’s
main (primary) memory. As the main storage is limited, internal sorting is
restricted to sort a small set of data items only. External sorting, on the
other hand, deals with a large number of items, which can’t be held comfortably
in main memory at once and hence reside separately. Internal sorting allows
more flexible approach in the structuring and accessing of the items, while
external sorting involves with a large number of to and fro data transfer between external
memory (low speed) and main memory (high speed). A classification of all
sorting principles is shown in Figure 14.2.

Fig. 14.2 Classification of sorting methods.
We
briefly discuss the principles behind each sorting techniques in the following
paragraphs.
Internal Sorting: All internal sorting techniques are based on two
principles:
· Sorting by comparison
· Sorting by distribution
Let
us discuss each principle briefly.
Sorting by comparison
Basic
operation involved in this type of sorting technique is comparison. A data item
is compared with other items in the list of items in order to find its place in
the sorted list. In other words, comparison is followed by arrangement. There are
four choices for doing that:
- Insertion
- Exchange
- Selection
- Enumeration
Insertion: From a given list of items, one item is considered at
a time. The item chosen is then inserted into an appropriate position relative
to the previously sorted items. The item can be inserted into the same list or
to a different list.
Exchange: If two items are found to be out of order, they are
interchanged. The process is repeated until no more exchange is required.
Selection: First the smallest (or largest) item is located and
it is separated from the rest; then the next smallest (or next largest) is
selected and so on until all item are separated.
Merge: Two or more input lists are merged into an output list and while
merging the items from an input list are chosen following the required sorting
order.
Sorting by distribution
In
this type of sorting, no key comparison takes place. All items under sorting
are distributed over an auxiliary storage space based on the constituent
element in each and then grouped them together to get the sorted list.
Distributions of items based on the following choices
- Radix
- Counting
- Hashing
Radix: An item is placed in a space decided by the bases (or radix) of its
components with which it is composed of.
Counting: Items are
sorted based on their relative counts.
Hashing: In this method, items are hashed, that is, dispersed
into a list based on a hash function (it is a calculation of a relative address
of the item).
The literature of sorting techniques is vast and it is
beyond the scope of this book to discuss all of them. We will discuss few
important of them. The major sorting techniques, which will be discussed in
this book are shown in Figure 10.3.
SORTING BY INSERTION
The
simple and memory efficient sorting method is based on the principle of
“sorting by insertion”. This sorting technique is based on the “bridge player”
method, that is, the way many bridge players sort there hands: picking up one
card at a time, place it into its right position, and so on. More specifically, assume that k1, k2, …, km
are the keys that have already been sorted, then we insert ki into a j-th
(![]() ) position in the previously sorted records such that
) position in the previously sorted records such that ![]() and
and ![]() , where
, where ![]() and
and ![]() are two keys in (j+1)-th and (j-1)-th positions, respectively in the list k1, k2,
…, km. Several variations
of this basic principle are possible, important of which includes the
following.
are two keys in (j+1)-th and (j-1)-th positions, respectively in the list k1, k2,
…, km. Several variations
of this basic principle are possible, important of which includes the
following.
· Straight insertion sort
· Binary insertion sort
· Two way insertion sort
· List insertion sort
In
the following sub sections, all these sorting methods are discussed in details.

Fig. 14.3 Classic sorting
techniques.
Straight Insertion Sort
This
is the simplest sorting method and usually referred to as insertion sort. Suppose N
keys are there in an input list. It requires N iterations to sort the entire list. We assume that the list after
sorting is stored into an another list, which we call as output list. Straight
insertion sort involves the following basic operations in any iteration j (0 ≤ j < N-1) when j number keys are there in the output
list such that K1 ≤ K2 ≤ K3…≤ Kj.
1.
Select the (j+1)-th key K from the input, which has to be inserted into the output list.
2.
Compare the key K with, Kj, Kj-1,
…, etc. in the output list successively (from right to left) until discovering
that K should be inserted between Ki and Ki+1, that is, ![]() .
.
3.
Move keys Ki+1, Ki+2 ,………, Kj in the output list up one space to the right.
4.
Put the key K into the position i+1.
This
is illustrated in Figure 14.4. The straight insertion sort method is precisely
defined in the form of an algorithm StraightInsertionSort.
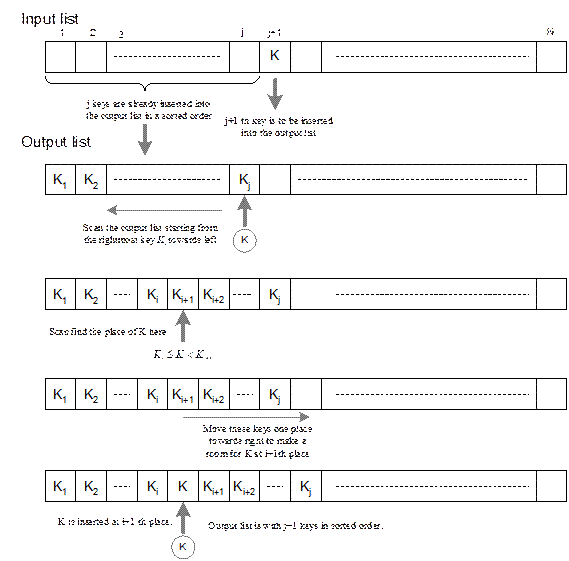
Fig. 14.4 Insertion sort at j-th iteration.
Algorithm StraightInsertionSort
Input: An input list A[1….N].
Output: An output list B[1….N].
Remark: Sorted
in ascending order.
Steps:
|
1. |
B[1]=A[1] // Initially first element in the
input list //
is the first element in the output list |
||||
|
2. |
For j = 2
to N do // Continue taking one key at a
time from the input list |
||||
|
|
/* Select
the key K from the input list */ |
||||
|
3. |
|
K = A[j] //
K is the key under insertion |
|||
|
|
/*
Search the location i in the output list such that |
||||
|
4. |
|
flag = TRUE // To control the
number of scan in the output list |
|||
|
5. |
|
i = j-1 // Points the rightmost
element in the output list |
|||
|
6. |
|
While (flag
= TRUE) do //
Scan until we get the place for K |
|||
|
7. |
|
|
If (K <
B[i]) then |
||
|
8. |
|
|
|
i = i-1 |
|
|
9. |
|
|
|
If (i = 0)
then
// Stop if the list is exhausted |
|
|
10. |
|
|
|
|
flag = FALSE |
|
11. |
|
|
|
EndIf |
|
|
12. |
|
|
Else |
||
|
13. |
|
|
|
flag = FALSE
// Stop here |
|
|
14. |
|
|
EndIf |
||
|
15. |
|
EndWhile |
|||
|
|
/* Move
to right one place all the keys from and after i+1 */ |
||||
|
16. |
|
p = j |
|||
|
17. |
|
While (p>i+1)
do |
|||
|
18. |
|
|
B[p] = B[p-1] |
||
|
19. |
|
|
p = p-1 |
||
|
20. |
|
EndWhile |
|||
|
|
/*
Insert the keys at i+1 th place */ |
||||
|
21. |
|
B[i+1] = K
// Insert the key at the (i+1)- th place |
|||
|
22. |
EndFor |
||||
|
23. |
Stop |
||||
Illustration
of the algorithm StraightInsertionSort
How
an input list A with 9 elements is
sorted by the algorithm StraighInsertionSort
is illustrated in Figure 10.5. In this example, N = 9. At the beginning, the first element, that is, A[1] = 5 is inserted into the array B, which is initially empty (this is
shown as iteration 0). In subsequent iterations
the algorithm selects the j-th
element (j = 2, 3, …, 9) from the
list A, goes on comparing with the
elements in B starting from the right most element of B to find its place. It then inserts at that place. We see that after j-th iteration, the (j+1)
number of elements are get sorted and stored in the output list B.
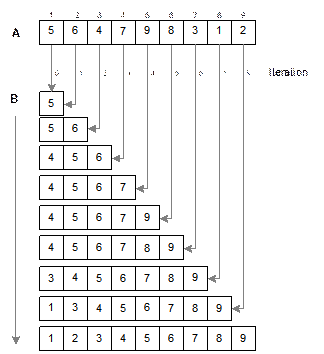
Fig. 14.5 Illustration of StraightInsertionSort algorithm.
Analysis of the algorithm
StraightInsertionSort
In
this section, we analyze the time and space complexities of the algorithm StraighInsertionSort. We consider
comparison and movement of data as the basic operations in the algorithm. We
analyze the complexities for the following three cases.
Case 1: The input list is
already in sorted order
Number of comparisons
In
this case, number of comparison in each iteration is 1. Total number of iteration
(For-loop in Step 2-22) required is n-1,
where n is the size of the list. Let C(n)
denotes the total number of comparisons to sort a list of size n. Therefore
![]() up to (n-1)-th iterations
up to (n-1)-th iterations
= n-1
Number of movements
In
this case, no data movement takes place in any iteration. Hence, number of
movement M(n) is
M (n) = 0
Memory requirement
In
this case, an additional storage space other than the storage space for the
input list is required to store the output list. Hence, the size of storage
space required to run the StraightInsertionSort
is
S(n) = n
Case 2: The input list is
stored but in reverse order
Number of comparisons
It
is observed that the i-th iteration requires i number of comparisons. Hence, considering
total n-1 iterations, we have
![]()
![]()
Number of movements
Number
of keys that needs to be moved in i-th
iteration is i. Therefore, total
number of key movements is
![]()
![]()
Memory requirement
Like
Case 1, here also we don’t need any extra storage space other than to store the
output list. Hence,
S(n) = n
Case 3: Input list is in
random order
Number of comparisons
Let
us consider the (i+1)-th iteration,
when i keys are there in the output
list and we want to insert the (i+1)-th
key into the list (where i = 0, 1, 2,
…, n-1). Note that in this case i number of elements are there in the
output list. Further, it can be noted that there are (i+1) locations where the key may go (see Figure 10.6). If ![]() be the probability that the key will go to the j-th location (0 ≤j ≤ i+1) then the number of comparisons will be
be the probability that the key will go to the j-th location (0 ≤j ≤ i+1) then the number of comparisons will be ![]() . Hence, the average number of comparisons in the (i+1)-th iteration is
. Hence, the average number of comparisons in the (i+1)-th iteration is
![]()
To simplify the analysis, let us assume that all keys
are distinct and all permutations of keys are equally likely. Then
![]()
Therefore, with this assumption,
we have the average number of comparisons in the (i+1)-th iteration as
![]()
= ![]()
=![]()
Hence,
total number of comparisons for all (n-1)
iterations is
![]()
=![]()
=![]()
=![]()
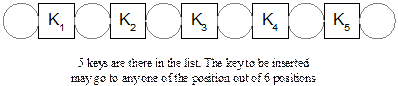
Fig. 14.6 Locations to place a
key at an iteration with five keys.
Number of movements
On
the average, number of movements in the i-th iteration can be calculated with
the same assumptions as in the case of calculation of number of comparisons is
![]() =
= ![]() (
(
Hence,
total number of movements M(n) to
sort a list of n numbers in random order is
![]()
=![]()
=![]()
Memory requirement
Like
Case 1 and Case 2, here is also the additional storage space required is
S(n) = n
From the analysis of the algorithm StraightInsertionSort, we can summarize
the results as shown in the Table 14.1.
Table 14.1 Analysis of the algorithm StraightInsertionSort.
|
Case |
Comparisons |
Movement |
Memory |
Remark |
|
Case 1 |
|
|
|
Input list is in sorted
order |
|
Case 2 |
|
|
|
Input list is sorted in
reversed order |
|
Case 3 |
|
|
|
Input list is in random
order |
The time complexity T(n) of the algorithm StraightInsertionSort
can be calculated considering the number of comparisons and number of movements, that is,
![]()
where
t1 and t2 denote the times
required for a unit comparison and movement, respectively. The time complexity
is summarized in the Table 10.2 assuming![]() , where c is a
constant.
, where c is a
constant.
Table 10.2 Time complexity of the
algorithm StraightInsertionSort.
|
Case |
Run time, T(n) |
Complexity |
Remark |
|
Case 1 |
|
|
Best case |
|
Case 2 |
|
|
Worst case |
|
Case 3 |
|
|
Average case |
List Insertion Sort
We
have seen that two major operations are involved in an iteration in straight
insertion sort: 1) scan the list to find the location of insertion and 2) move
keys to accommodate the key. Straight insertion sort assumes that the list of
keys is stored in an array that is, using sequential storage allocation. The problem
with this data structure is that it is necessary to move a large number of keys
(on the average, half number of keys in an iteration) in order to accomplish
each insertion operation. In contrast to this, we know that linked allocation
is ideally suited for insertion, since only a few links need to be changed, and
the other operation namely, scanning with linked allocation is as easy as with
sequential allocation. These two observations leads to another variation of the
straight insertion sort called list insertion sort. Only one way linkage, that
is, single linked list structure is enough for the purpose because we always
scan the list in the same direction. We
consider input list is stored in an array and the output list is maintained
with the single linked list structure.
Following
steps are there in an iteration in the list insertion sort to insert a node.
- Allocate memory for a node
to be inserted.
- Scan the list to the
right starting from the header node in the output list to find its place
of insertion.
- Insert the node.
The list insertion sort is illustrated in Figure 14.7.
Figure 14.7 shows insertion of a key K
into the output list in i-th
iteration. The output list is with the header node HEADER. Suppose,![]() , where Kj
and Kj+1
are the two keys in two consecutive nodes in the list prior to the
insertion. The list insertion sort technique is precisely defined in the
algorithm ListInsertionSort.
, where Kj
and Kj+1
are the two keys in two consecutive nodes in the list prior to the
insertion. The list insertion sort technique is precisely defined in the
algorithm ListInsertionSort.

Fig. 14.7 List insertion sort.
Algorithm ListInsertionSort
Input: An input list is stored in an array A[1….N].
Output: Elements are sorted in ascending order.
Remark: A one way single linked list with HEADER as the pointer to the header node
as the output list.
Steps:
|
|
/* Initially
first element is in the input list is the first element in the output list */ |
|||
|
1. |
HEADER→DATA=NULL, HEADER→LINK=NULL
// Initially start with the
empty list |
|||
|
|
// Get a new node for the
first element in the input list // |
|||
|
2. |
new = GetNode(), new→DATA = A[1], new→LINK = NULL |
|||
|
3. |
HEADER→LINK = new // Insert the new node
at the front |
|||
|
4. |
For j = 2
to N do // Continue taking one key at a
time from the input list |
|||
|
|
/*
Select the key K from the input list */ |
|||
|
5. |
|
K = A[j] //
K is the key under insertion |
||
|
|
|
// Get a new node to store
the key K // |
||
|
6. |
|
new = GetNode(),
new→DATA = K, new→LINK = NULL |
||
|
|
/*
Search the location in the output list such that |
|||
|
7. |
|
ptr1 = HEADER, ptr2 = HEADER→LINK // Start from the
header node |
||
|
|
|
flag = TRUE // To
control the scan in the output list |
||
|
6. |
|
While
(flag = TRUE) and (ptr2 |
||
|
7. |
|
|
If (ptr2→DATA
|
|
|
8. |
|
|
|
ptr2 = ptr2→LINK, ptr1 = ptr1→LINK |
|
9. |
|
|
Else
|
|
|
10. |
|
|
|
flag = FALSE // Place of insertion is found here |
|
11. |
|
|
EndIf |
|
|
12. |
|
EndWhile |
||
|
13. |
|
ptr1→LINK = new,
new→LINK = ptr2 // Insert the
node with key K here |
||
|
14. |
EndFor |
|||
|
15. |
Stop |
|||
Illustration
of the algorithm ListInsertionSort
Figure 14.8 shows how the
input list A with 9 items in it are
sorted by the list insertion sort method. If we trace the list insertion sort,
it will go through the following 8 iterations shown in Figure 14.8.
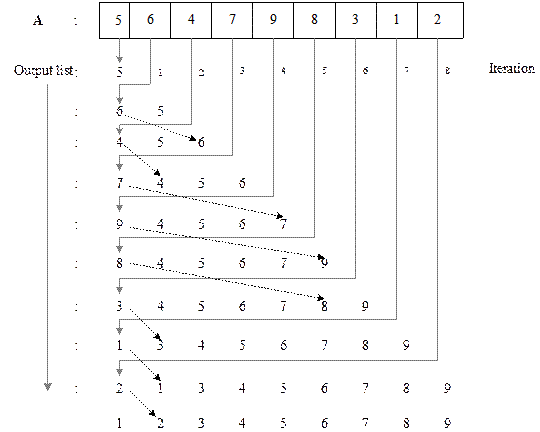
Fig. 14.8 Illustration
of the algorithm ListInsertionSort.
Analysis of the algorithm
ListInsertionSort
Let
us analyze the time and space complexities of the algorithm ListInsertionSort. We consider the
operation comparison as the basic operation in the algorithm. The algorithm ListInsertionSort is analyzed for the
following three cases.
Case 1: The input list is already in sorted order
Number of comparisons
In
this case, number of comparisons in the i-th
iteration is i (because i number of elements are there in the
output list). Now, total number of iterations (see For-loop in Step 4-14)
required in the algorithm is n-1,
where n is the size of the input list.
Let C(n) denotes the total number of comparisons to sort a list of size n. Then
![]()
= ![]()
Number of movements
This
technique does not require any data movement unlike the straight insertion sort.
However, the algorithm requires changes in two link fields. We can consider one
change in link field is equivalent to one movement operation. With this
consideration, the number of movements M(n)
stands as
M (n) = 2
Memory requirement
This
method needs to maintain (n+1) nodes
including the header node to maintain the output list with n key values. Let us consider that a node needs three units (one
unit for key and two units for the link field) memory space to hold a key. Then
the size of storage space required is
S(n) = 3(n+1)
Case 2: The input list is sorted but in reverse order
Number of comparisons
In
this case any iteration requires exactly one comparison. Hence, considering
total n-1 iterations, we have
![]() up to n-1 terms
up to n-1 terms
![]()
Number of movements
Number
of key movements is same as in the Case 1 of this technique. Therefore, total number
of key movements is
![]()
Memory requirement
Like
Case 1 of this algorithm, storage space required in this case is
S(n) = 3(n+1)
Case 3: Input list is
randomly ordered
Number of comparisons
Let
us consider the i-th iteration, when i keys are there in the output list and
we want to insert the (i+1)-th key
into the list (see Figure 10.8). This key can be inserted in any location such
as at front, at end or after the j-th
node from the front. There is only one comparison, if the key is inserted at
front. There are i number of
comparisons when the key is inserted at the end. Similarly, j number of comparisons are required to insert
the key after the j-th node (![]() ). Assuming that all
keys are distinct and all permutations of keys are equally likely, number of
comparisons required to find the place of insertion of (i+1)-th key at any i-th
iteration, on the average is
). Assuming that all
keys are distinct and all permutations of keys are equally likely, number of
comparisons required to find the place of insertion of (i+1)-th key at any i-th
iteration, on the average is
![]()
= ![]()
= ![]()
Total
number of comparisons for all (n-1)
iterations is
![]()
=![]()
=![]()
=![]()
![]()
Number of movements
Number
of key movement is same as in the Case 1 and Case 2 of this technique.
Therefore, total number of key movements is
![]()
Memory requirement
Like
Case 1 and Case 2 of this algorithm, storage space required is
S(n) = 3(n+1)
(
The analysis of the algorithm ListInsertionSort is summarized in Table 14.3.
Table 14.3 Analysis of the
algorithm ListInsertionSort.
|
Case |
Comparisons |
Movement |
Memory |
Remark |
|
Case 1 |
|
|
|
Input list is in sorted
order |
|
Case 2 |
|
|
|
Input list is sorted in
reversed order |
|
Case 3 |
|
|
|
Input list is in random
order |
With the same convention as followed in the time
complexity of the algorithm StraightInsertionSort,
the time complexities of the algorithm ListInsertionSort
is furnished in Table 14.4.
Table 14.4 Time complexity of the algorithm ListInsertionSort.
|
Case |
Run time T(n) |
Complexity |
Remark |
|
Case 1 |
|
|
Worst case |
|
Case 2 |
|
|
Best case |
|
Case 3 |
|
|
Average case |
Note: From the analysis of the ListInsertionSort algorithm, we can see that list insertion sort
has the best case performance when the input list is sorted but in reversed
order. It performs better than the average case when the list is already
sorted. Further, on the average, the performance of ListInsertionSort algorithm is comparable to that of the StraightInsertionSort algorithm.
Binary
Insertion Sort
Another
variation of insertion sort namely, binary insertion sort is known to reduce
the number of comparisons further. In straight insertion sort, at any i-th pass, we scan the output list starting
from the left (may be also from the right) to the opposite end. The binary
insertion sort, however, suggest to probe first at the middle of all keys instead
of at an end. Let the key value at the middle be Km. and the key value to be inserted be K at the i-th iteration. The search for the
insertion location of K stops, or
repeat probes at the left half or right half depending on ![]() ,
, ![]() or
or ![]() , respectively. For Example, when inserting the 64th
record, We can start by comparing K64
with K32; if it is less,
we compare it with K16,
but if it is greater, we compare it with K48 etc. Figure 10.9 shows
the likely probes in binary insertion sort technique on a list at an i-th iteration, that is, when the list
contains i-1 (i>1) number of keys. This type of probing is popularly known as
“binary search”, which will be discussed in details in Chapter 11.
, respectively. For Example, when inserting the 64th
record, We can start by comparing K64
with K32; if it is less,
we compare it with K16,
but if it is greater, we compare it with K48 etc. Figure 10.9 shows
the likely probes in binary insertion sort technique on a list at an i-th iteration, that is, when the list
contains i-1 (i>1) number of keys. This type of probing is popularly known as
“binary search”, which will be discussed in details in Chapter 11.

Fig. 14.9 Possible probes in binary insertion sort.
Binary insertion sort goes through the following steps
at any iteration to insert a key K.
- Search the
list to find the location of the key K
to be inserted. Let the location be j.
- Shift all key
values starting from the location j one
place to right to make room for K
at j.
- Insert the
key K at j.
The detail steps in the
binary insertion sort are described in the algorithm BinaryInsertionSort.
Algorithm BinaryInsertionSort
Input: A
list of N items stored in an array A[1….N].
Output: A
list of sorted items stored in B[1…N].
Remark:
Sorted in ascending order.
Steps:
|
1. |
B[1] = A[1] // Initially the
first element is inserted without any comparison |
||
|
2. |
For j = 2
to N do // Continue
taking one key at a time from the input list A |
||
|
3. |
|
K = A[j]
// The next element to
be inserted |
|
|
|
|
/* Search the list to find the location for the key
K */ |
|
|
4. |
|
L =1; R = j-1 // Two
pointers to the two ends of the output list B |
|
|
5. |
|
loc = BinarySearch(K, L, R) // Call the probe to find the place of
insertion of K |
|
|
|
|
/* Move the keys starting from the location “loc” */ |
|
|
6. |
|
i = j-1 |
|
|
7. |
|
While (i >
loc) do |
|
|
8. |
|
|
B[i+1] = B[i] |
|
9. |
|
|
i = i - 1 |
|
10. |
|
EndWhile |
|
|
11. |
|
B[i+1] = K //
Insert the key at “loc” |
|
|
12. |
EndFor |
||
|
13. |
Stop |
||
The BinarySearch(…) procedure
referred in Step 5 is defined below.
Algorithm BinarySearch
Input: K, the key value whose place of insertion
to be searched, L and R are the left and right indices of the array B.
Output:
Return the location loc such that B[loc]
≤ K< B[loc].
Remark:
Binary search over the array B, which
is global to the procedure; the algorithm is defined
recursively.
Steps:
|
1. |
If (R |
||
|
2. |
|
If (B[L]
> K) then |
|
|
3. |
|
|
loc = L-1 |
|
4. |
|
|
Return(loc) |
|
5. |
|
Else |
|
|
6. |
|
|
loc = L |
|
7. |
|
|
Return(loc) |
|
8. |
|
EndIf |
|
|
9. |
EndIf |
||
|
10. |
mid = |
||
|
11. |
If (K < B[mid] ) then |
||
|
12. |
|
R = mid -1 |
|
|
13. |
|
loc = BinarySearch(K, L, R)
//
Recursive search at left half |
|
|
14. |
|
Return(loc) |
|
|
15. |
EndIf |
||
|
16. |
If (K > B[mid]) then |
||
|
17. |
|
L = mid+1 |
|
|
18. |
|
loc = BinarySearch(K, L, R)
//
Recursive search at right half |
|
|
19. |
|
Return(loc) |
|
|
20. |
EndIf |
||
|
21. |
If (K = B[mid]) then |
||
|
22. |
|
loc = mid //
Element is found here |
|
|
23. |
|
Return(loc) |
|
|
24. |
EndIf |
||
|
25. |
Stop |
||
Illustration of Binary Insertion Sort
How
the binary insertion sort searches for the place of insertion in an iteration is
shown in Figure 14.10. Assume that at that iteration the list B contains 6 keys and 3 is the key to be
inserted into it.

Fig. 14.10 Insertion in binary insertion sort.
Analysis
of the algorithm BinaryInsertionSort
Binary
insertion sort and the straight insertion sort differ in the way they perform
the search to find the location of insertion. The straight insertion sort follows
simple sequential search starting from the rightmost (or leftmost) key in the
output list, whereas the binary insertion sort performs binary search over the
keys in the output list. Except this difference in searching procedures the two
sorting techniques are same. Hence, to analyze the BinaryInsertionSort algorithm we consider the number of comparisons
involved in the binary insertion sort only.
Case 1: When the input list is sorted but in reverse order
Let
us consider the situation of i-th
pass in this case. We note that in i-th
pass i
number of keys are there in the list, and (i+1)-th
key is to be inserted. It can be observed that binary search always probes at
the left side of the output list in this case. To make the discussion simple,
let us assume that ![]() , where k is a constant. With this assumption it can be noted
that the binary search probes at locations 2k-1, 2k-2,…, 20.
, where k is a constant. With this assumption it can be noted
that the binary search probes at locations 2k-1, 2k-2,…, 20.
Hence, the number of
comparisons in i-th pass is ![]()
There
is total n-1 iterations required.
Therefore, total number of comparisons to sort the list of n numbers is given by
![]()
= ![]()
= ![]()
Case 2: When the input list is in sorted order
This case is similar to the
Case 1 except that the binary search probes at the right side of the output
list always. Hence, arguing in the same as way in Case 1, the number of comparisons
is
![]()
Case 3: When the keys in the input list are in random order
We
have seen that in binary search, maximum number of key comparisons takes place
in Case 1 and Case 2, which is = ![]() in iteration i.
This is also same as the number of maximum probing locations. If all keys are
distinct and equally probable in any position in the list, then the probability
that a key will be in any one of this location is
in iteration i.
This is also same as the number of maximum probing locations. If all keys are
distinct and equally probable in any position in the list, then the probability
that a key will be in any one of this location is
![]()
Therefore, on the average,
number of key comparisons in i-th
iteration is
![]() where j.p counts the probability that the key
will be found at j-th probe.
where j.p counts the probability that the key
will be found at j-th probe.
= ![]()
Hence, total number of key comparisons
to sort n keys in this case is given
by
![]()
=![]()
= ![]()
As pointed out in previous discussion, BinaryInsertionSort is same as the StraightInsertionSort except the search procedures;
hence the number of movements and amount of auxiliary storage space in the
algorithm BinaryInsertionSort remains
same as in the StraightInsertionSort
algorithm. The analysis of the algorithm BinaryInsertionSort
is now summarized in Table 14.5.
Table 14.5 Analysis of the algorithm BinaryInsertionSort.
|
Case |
Comparisons |
Movement |
Memory |
Remark |
|
Case 1 |
|
|
|
Input list is in sorted
order |
|
Case 2 |
|
|
|
Input list is sorted in
reversed order |
|
Case 3 |
|
|
|
Input list is in random
order |
Considering the Stirling’s approximation (Appendix A,
A.1.13) we can write ![]() and with the same convention as followed in the time
complexity of the previously discussed algorithms, the time complexities of the
algorithm BinaryInsertionSort is
furnished in Table 14.6.
and with the same convention as followed in the time
complexity of the previously discussed algorithms, the time complexities of the
algorithm BinaryInsertionSort is
furnished in Table 14.6.
Table 14.6 Time complexity of the algorithm BinaryInsertionSort.
|
Case |
Run time T(n) |
Complexity |
Remark |
|
Case 1 |
|
|
Best case |
|
Case 2 |
|
|
Average case |
|
Case 3 |
|
= |
Worst case |
Note: We could improve the complexity of the BinaryInsertionSort algorithm if the
output list is maintained with a single linked list structure instead of an
array. But binary search can not be implemented with the linked list structure.
Nevertheless, BinaryInsertionSort
performs better than the StraightInsertionSort
as lesser number of comparisons is involved in BinaryInsertionSort. In other words, if we consider the movements
of data into account, the BinaryInsertionSort
is better compared to the StraightInsertionSort.
Further, the merit of lesser number of comapariosons in BinaryInsertionSort may be qwestinable to that of movement operations
in ListInsertionSort algorithm.
SORTING BY
SELECTION
In
this section, we introduce another family of sorting technique based on the
principle of selection. In case of insertion sorting techniques it is not
necessary that all keys to be sorted should be available before sorting starts.
The key values are read from the keyboard or a file one at a time while the
sorting procedure continues. It can be noted that a pass in the insertion
sorting reads a key and put it into the output list, which is sorted with key
values read so far. In contrast to this, the selection sort requires all keys
under sorting are available prior to the execution. Further, selection sort considers following
two basic operations.
Select: Selection of an item from the input list.
Swap:
Interchange two items in the list.
In selection sorting, the above two steps are iterated
to produce the sorted list, which progress from one end as the iteration
continues. We may note that selection sorting can be done on the input list
itself. This implies that selection sort is an in place sorting technique.
Different variations of sorting based on this
principle are available in the literature. Important of them and which are
included in this book is listed below.
1. Straight selection sort
2. Tree sort
3. Heap sort
Above mentioned three sorting techniques are discussed
in full length in the following sub-sections.
Straight
Selection Sort
The
simplest “sorting by selection” technique is the straight selection sort.
Suppose, n number of key values are
there in the list to be sorted. This
technique requires n-1 iterations to
complete the sorting. Let us consider the case of i-th iteration, where 1≤ i<n. The i-th iteration
begins with i-1 keys say, ![]() which are already in
sorted order. Two basic steps in each iteration are as follows.
which are already in
sorted order. Two basic steps in each iteration are as follows.
Select:
Select the smallest key in the list of remaining key values say, ![]() .Let the smallest key value be
.Let the smallest key value be ![]()
![]() .
.
Swap:
Swap the two key values Ki
and Kj.
An
iteration in the straight selection sort is illustrated in Fig. 14.13. The
straight selection sort is more precisely defined in the form of pseudo code as
shown in the algorithm StraighSelectionSort.
Algorithm StraightSelectionSort
Input: An
input list A[1…N].
Output: The
list A[1…N] in sorted order.
Remark:
Sorted in ascending order.
Steps:
|
1. |
For i = 1
to (n-1) do //
(n-1) iterations |
||
|
2. |
|
j = SelectMin(i, n) // Select the
smallest from the remaining part of the list |
|
|
3. |
|
If (i ≠ j) then // Interchange
when the minimum is in remote |
|
|
4. |
|
|
Swap(A[i],
A[j]) |
|
5. |
|
EndIf |
|
|
6. |
EndFor |
||
|
7. |
Stop |
||
The procedure SelectMin(i, n)
is to find the smallest element
in the list between the location i
and n both inclusive, which is
described as the algorithm SelectMin
below. The procedure to perform the swap operation between the data value X
and Y are described in the algorithm Swap.

Fig. 14.13 Illustration of the
straight selection sort.
Algorithm SelectMin
Input: A list in the form of an array of size n with L (left) and R (right) being the selection range,
where![]() .
.
Output: The index of array A where the minimum is located
Remark: If the list contains more than one minimum then it
returns the index of the first occurrence.
Steps:
|
1. |
min
= A[L]
// Initially, the item at the
starting location is chosen as the smallest |
||
|
2. |
minLoc = L
// minLoc record the location
of the minimum |
||
|
3. |
For i =
L+1 to R do
// Search the entire part |
||
|
4. |
|
If (min >
A[i]) then |
|
|
5. |
|
|
min = A[i] // Now
the smallest is updated here |
|
6. |
|
|
minLoc
= i //
New location of the smallest so far |
|
7. |
|
EndIf |
|
|
8. |
EndFor |
||
|
7. |
Return(minLoc) // Return
the location of the smallest element |
||
|
9. |
Stop |
||
Algorithm Swap
Input: X and Y are two variables.
Output: The value in X
goes to Y and vice-versa.
Remark:
X and Y should be passed as pointers.
Steps:
|
1. |
temp
= X
// Store the value in X in a temporary storage space |
|
2. |
X = Y
// Copy the value of Y to X |
|
3. |
Y = temp
// Copy the value in temp to Y |
|
4. |
Stop |
An
alternative implementation of the swap operation without using temporary
storage is given below.
Algorithm Swap
Input: X and Y are two variables.
Output: The value in X
goes to Y and vice-versa.
Remark: X and Y should be passed as pointers. It does
not require any temporary storage space.
|
1. |
X = X + Y
// X
holds total of the both the values |
|
2. |
Y
= X – Y
// Y now holds the previous value of X |
|
3. |
X
= X – Y
// X
now holds the previous value of Y |
|
4. |
Stop |
Illustration of the algorithm StraightSelectionSort
Figure
10.14 illustrates the straight selection sort for an array A with 9 elements stored in it. The algorithm in this case requires
8 passes as shown.

Fig. 10.14 Continued.

Fig. 14.14
Illustration of the algorithm StraightSelectionSort.
Analysis
of the algorithm StraightSelectionSort
Let
us analyze the time and space complexities of the algorithm StraightSelectionSort. It can be noted
that the straight selection sort performs the sorting on the same list as the
input list. Hence, it is an in place
sorting technique. In other words, the
straight selection sort does not require additional storage space other than
the space to store the input list itself. In our subsequent discussions on the
analysis of this sorting technique, we therefore legitimately assume S(n), the storage space required to sort
n element is zero. The algorithm StraightSelectionSort is analyzed for
the following three cases.
Case 1: The input list is
already in sorted order
Number of comparisons
The
algorithm StraightSelectionSort
requires total (n-1) iterations (see
Step 1 in the algorithm StraightSelectionSort)
and for each the SelectMin(…)
function is invoked. Now let us consider the case of the i-th iteration. It is evident that in the i-th iteration, (i-1)
items are already sorted and SelectMin(…)
function searches for the minimum in
remaining ![]() elements. To do this,
it needs
elements. To do this,
it needs ![]() number of comparisons
(see Steps 3 and 4 in the algorithm SelectMin(…).
Therefore, considering all iteration from 1 to (n-1), total number of comparisons required is given by
number of comparisons
(see Steps 3 and 4 in the algorithm SelectMin(…).
Therefore, considering all iteration from 1 to (n-1), total number of comparisons required is given by
![]()
= ![]()
= ![]()
Number of movements
In
this case no swap operation is involved since the input is in sorted order.
Hence, the number of movements is
M (n) = 0
Memory requirement
S(n) = 0
Case 2: The input list is stored but in reverse order
Number of comparisons
Like
the Case 1 analysis of the sorting algorithm under discussion, we can calculate
the number of comparisons ![]() to sort n items
is
to sort n items
is
![]()
Number of movements
Students
are advised to trace the execution of the algorithm StraightSelectionSort before getting the number of movements in
this case. It can be observed that when the list is in reverse order, there are
movements of data until the half part of the list is sorted. When we have done just
sorting half of the list, elements in the rest (unsorted) part are already in
their final positions and hence no data movements occur. Therefore, Swap(…) operation takes place only in
the first ![]() iterations. Further, a
single swap operation is associated with 3 data movement (considering the first
version of the Swap(…), with temporary copy). Therefore, the
number of movements required with a list of size n and when it contains the elements in reverse order is
iterations. Further, a
single swap operation is associated with 3 data movement (considering the first
version of the Swap(…), with temporary copy). Therefore, the
number of movements required with a list of size n and when it contains the elements in reverse order is
![]()
Memory requirement
S(n) = 0
Case 3: Elements in the input
list are in random order
Number of comparisons
Number
of comparisons required in this case is also same as in the last two cases of
the algorithm. Hence,
![]()
Number of movements
Straight
selection sort does not perform any swap operation, if the i-th smallest element is present in the i-th location. Let ![]() be the probability
that the i-th smallest element is in
the i-th position. Hence, the
probability that there will be a swap operation in the i-th pass is
be the probability
that the i-th smallest element is in
the i-th position. Hence, the
probability that there will be a swap operation in the i-th pass is ![]() . So, on the average,
number of swaps in (n-1) total iterations
is
. So, on the average,
number of swaps in (n-1) total iterations
is
![]()
To simplify the analysis, let us assume that all keys
are distinct, and all permutations of keys are equally likely as input. Then we
have
![]()
With this assumption and considering that there are
three data movements in a swap operation, the average number of movements in
the algorithm StraightSelectionSort
becomes
![]() =
= ![]()
Memory requirement
Like
Case 1 and Case 2 of this algorithm, storage space required is
S(n) = 0
From the analysis of the algorithm StraightSelectionSort, we can summarize
the results as shown in Table 14.8.
Table 14.8 Analysis of the algorithm StraightSelectionSort.
|
Case |
Comparisons |
Movement |
Memory |
Remark |
|
Case 1 |
|
|
|
Input list is in sorted
order |
|
Case 2 |
|
|
|
Input list is sorted in
reverse order |
|
Case 3 |
|
|
|
Input list is in random
order |
The
time complexity T(n) of the algorithm
StraightSelectionSort can be
calculated considering the number of comparisons and number of movements, that is,
![]()
where
t1 and t2 denote the times for a
single comparison and movement, respectively.
Table
14.9 shows the run time complexity of the algorithm in three different
situations of the input list.
Table 14.9 Time complexity of the algorithm StraightSelectionSort.
|
Case |
Run time, T(n) |
Complexity |
Remark |
|
Case 1 |
|
|
Best case |
|
Case 2 |
|
|
Average case |
|
Case 3 |
(Taking |
|
Worst case |
Note: From the analysis of the straight selection sort, it
is evident that number of comparisons is independent of the ordering of
elements in the input list. However, the performance of the algorithm varies
with respect to the number of movements involved. For the sake of simplicity,
let us consider the large value of n,
such that![]() . With this consideration, number of movements require in
Case 2 is
. With this consideration, number of movements require in
Case 2 is ![]() and in Case 3 is 3n.
Thus, Case 2 is better compared to the Case 3. Therefore, we can term the best
case execution of the algorithm when the input list is sorted and worst case
when the input list is in random order.
and in Case 3 is 3n.
Thus, Case 2 is better compared to the Case 3. Therefore, we can term the best
case execution of the algorithm when the input list is sorted and worst case
when the input list is in random order.
Heap Sort
J.
W. J. Williams in Communication of ACM,
347-358, 1964, introduced the idea of an alternative selection strategy. Based
on this strategy another “sorting by selection” technique is known called heap sort. Like the tree selection sort,
heap sort follows a complete binary tree to maintain n key values and unlike it does not store “holes” containing
–α. The heap sort is treated as the best sorting technique in the category
of selection sorting. This sorting is termed as “heap” sort because it uses the
heap data structures. A complete discussion on heap data structure is available
in Section 7.5.3 in this book. We shall quickly review few important properties
of the heap data structure which will be frequently referred in our subsequent
discussions.
Heap tree
A
heap tree is a complete binary tree and stored in an array. Each node of the
heap tree stores a key value under sort. In Figure 14.21, a heap tree with 10
keys and its array representation (A)
is shown. It can be noted that the heap tree is completely filled in its all
levels except possibly the lowest, which is filled from the left to right. The
root of the tree is A[1] and given
the index i of a node, the index of
its parent, left child and right child can be computed using the following
rules.
Parent(i)
= i/2 // If the node is at i then its parent is at i/2
Left child(i)
=2i // If the parent is at i then its left child is at 2i
Right child(i)
= 2i+1
// If the parent is at i then its right child is at 2i+1
Further, it can be noted that any complete binary tree
is not necessarily a heap tree. A heap tree must satisfy an ordering property,
called the heap property. The heap
property specifies the ordering between the values at any node and the values
in any node in the sub trees of that node. There are two kinds of heaps: max
heap and min heap. The max heap property is stated below.
Max heap property: A[Parent(i)] ≥ A[i] for
all node i except the root node
That
is, the value of a node is at most the value of its parent. In other word, in a
max heap, the largest element is stored at the root. The heap tree that is
shown in Fig. 14.21 is satisfying the max heap property and such a heap tree is
specially termed as the max heap tree.
Similarly,
the min heap tree can be obtained satisfying the min heap property, which is
stated below.
Min heap property: A[Parent(i)] ≤ A[i]
for all node i except the root node
In
this case , the smallest value is at the root and the sub tree rooted at a node
contains value no smaller than that contained at the node itself.
Note that the heap property is true for every node in
the heap tree except the root node since root does not have any parent.
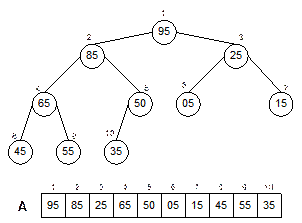
Fig. 14.21 A heap tree and its
array representation.
Sorting using heap tree
As
mentioned earlier, the heap sort uses heap tree as an underlying data structure
to sort an array of elements. The heap sort, unlike the tree selection sort is
an in place sorting method, because it does not require any extra storage space
other than the input storage list. Let us consider the case of sorting n elements stored in an array A[1, 2, …, n]. We assume that heap tree satisfies the property of max heap unless
otherwise stated. The basic steps in the heap sort are list below.
- Create heap: Create the initial heap tree with n elements stored in the array A.
For i = n down to 1 do
- Remove max: Select the value in the root node (this is the maximum value in
the heap). Swap the values (that is A[1])
and value at the i-th location
in A.
- Rebuild heap: Rebuild the heap tree for elements A[1, 2, …, i-1 ].
We see that in addition to the basic operations
namely, select and swap (Step 2), this sorting method requires two additional
operations, namely create heap and rebuild heap. The first is done once while
the later is done n times. Fig. 14.22
illustrates the basic steps involved in heap sort and different sub steps in an i-th
iteration.
Now we discuss the details about each step in the heap
sort.
Create heap
Given
a list of items stored in array A, we
are to rearrange them into another array say, B (it is the array representation of the heap tree) so that each
element satisfies the heap property. For an example, an input list A with 10 elements in random order and
heap B after the create heap
operation is shown in Fig. 14.23.
The create heap procedure is comprised of
the following steps.
Initially, the heap tree (B) is empty and iteration i
= 1.
1. Select the i-th
element from the list A. let this
element be x.
2. Insert the
element x into B satisfying the heap property with the following step.
2.1 Let j = i. Add the element at
the j-th place in the array B.
2.2 Compare x
with Parent[j] and swap if it violates
the heap property else exit.
2.3 Move to the parent of Parent[j], that is, j = j/2 and repeat the Step 2.2
3. i = i + 1.
Go to step 1.
The
create heap operation is illustrated in Figure 14.23.

Fig. 14.22 Illustration of the
heap sort.

Fig. 14.23 Create heap: input
array A to heap B.
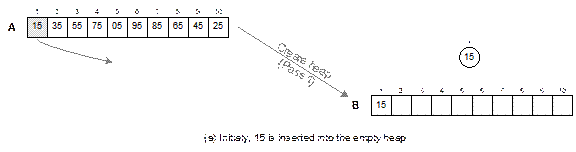
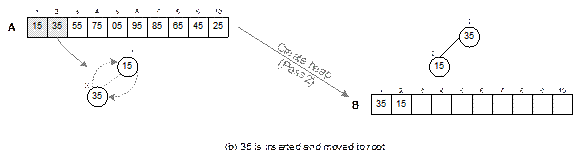


Fig. 14.24
Continued.
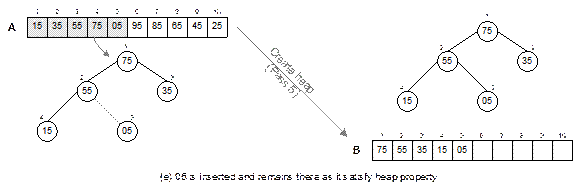

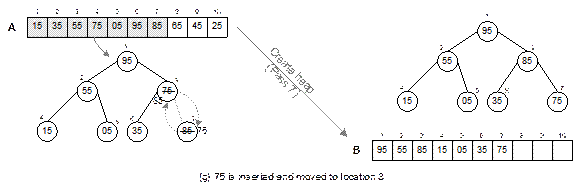

Fig. 14.24
Continued.
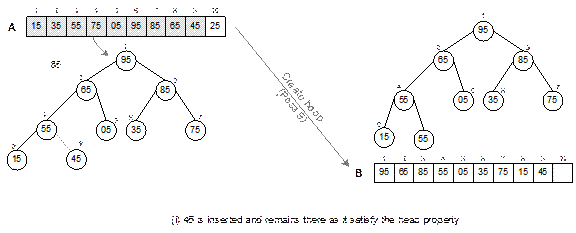

Fig. 14.24 Illustration of create
heap operation.
The create heap operation is precisely defined as the
algorithm CreateHeap.
Algorithm CreateHeap
Input: A[1, 2, …, n] an array of n items.
Output: B[1,
2, …, n] stores the heap tree.
Remark:
Creates heap with max heap property.
Steps
|
1. |
i = 1 //
Initially, the heap tree (B) is empty and start with first element in A |
||
|
2. |
While (i
≤ n) do //
Repeat for all elements in the array A |
||
|
3. |
|
x = A[i]
// Select the i-th element from
the list A |
|
|
4. |
|
B[i] = x // Add the element at
the i-th place in the array B |
|
|
5. |
|
j = i
// j is the current location of the element in B |
|
|
6. |
|
While (j
> 1) do // Continue
until the root is checked |
|
|
7. |
|
|
If B[j]
> B[j/2] then
// It violates the heap (max) property |
|
8. |
|
|
temp = B[j]
//
Swap the elements |
|
9. |
|
|
B[j] = B[j/2] |
|
10. |
|
|
B[j/2] = temp |
|
11. |
|
|
j = j/2
// Go to the parent node |
|
12. |
|
|
Else |
|
13. |
|
|
j = 1 //
Satisfy heap property, terminates this inner loop |
|
14. |
|
|
EndIf |
|
15. |
|
EndWhile |
|
|
|
|
i = i +1
// Select the next element from the input list |
|
|
16. |
EndWhile |
||
|
17. |
Stop |
||
Remove Max
Once
a heap is created the largest element appears at the root node. In our sorting
procedure, we select this element and move this into the output list. In heap
sort, it is possible to store the output list in the same array as the heap
tree. So selecting the element from the root and move it to the output list
implies the swapping this element with the last element in the heap. Here, last
element in the heap means the right most element at the last level. The remove max
operation is illustrated in Figure 14.25.

Fig. 14.25 Illustration of the remove max operation.
From Figure 14.25, it is evident that the remove
operation basically a swap operation between the root and the last element in
the heap. This operation is defined in algorithm RemoveMax.
Algorithm RemoveMax
Input: B[1, 2, …, n] an array of n items and the last element in the heap
is at i .
Output: The
first element and the i-th element gets
interchanged.
Steps:
|
1. |
temp = B[i] // Swap the elements |
|
2. |
B[i] = B[1] |
|
3. |
B[1] = temp |
|
4. |
Stop |
Rebuild heap
The
remove max operation may result the heap, which violates the heap property.
This is because the last element placed at the root is not necessarily the
largest element. So it is necessary to rebuild the heap satisfying the heap
property. The rebuild operation is very simple. The steps in the rebuild
operation are listed below and illustrated in Figure 10.26 and defined in
details in the algorithm RebuildHeap.
Let
the heap is in the array B[1, 2, …,
i].
- Start with the root
and j = 1.
- If j-th and left child (at 2*j-th location) violate the heap
property then swap them. Else if j-th
and right child (at 2*j+1-th
location) violate the heap property then swap them, else no rebuild is
required and exit.
- Move down to the next
level, that is, j = 2*j if swap takes place with left
child. Else j = 2*j+1.
- If (j > i ), rebuild is done
and exit; else go to Step 2.

Fig. 14.26 Illustration of the rebuild operation.
Algorithm RebuildHeap
Input: B[1, 2, …, i] an array and the last
element in the heap under rebuild is at i.
Output: The
heap satisfying the heap property.
Remark: Heap
is assumed as the max heap.
Steps:
|
1. |
If (i = 1)
then |
||||
|
2. |
Exit //
No rebuild with single element in the list |
||||
|
3. |
j = 1
// Else start with the root node |
||||
|
4. |
flag = TRUE
// Rebuild is required |
||||
|
5. |
While
(flag = TRUE) do |
||||
|
6. |
|
leftChild = 2*j, rightChild
= 2*j+1 |
|||
|
|
|
/* Check if the right child
is within the range of heap or not */ |
|||
|
|
|
// Note: If right
child is within the range then also left child |
|||
|
7. |
|
If
(rightChild |
|||
|
8. |
|
|
/* Compare whether left or
right child will move to up or not */ |
||
|
9. |
|
|
If (B[j]
// Parent and left violate heap property |
||
|
10. |
|
|
|
Swap(B[j],
B[leftChild]) //
Swap parent and left child |
|
|
11. |
|
|
|
j = leftChild
// Move down to node at the next level |
|
|
12. |
|
|
Else |
||
|
13. |
|
|
|
If (B[j]
// Parent and right violate heap property |
|
|
14. |
|
|
|
|
Swap(B[j],
B[rightChild])
// Swap parent and right child |
|
15. |
|
|
|
|
j = rightChild // Move down to node at the next level |
|
16. |
|
|
|
Else // Heap property
is not violated |
|
|
17. |
|
|
|
|
flag = FALSE |
|
18. |
|
|
|
EndIf |
|
|
19. |
|
|
EndIf |
||
|
20. |
|
Else //
Check if the left child is within the range of heap or not |
|||
|
21. |
|
|
If (leftChild
≤ i) then |
||
|
22. |
|
|
|
If (B[j] |
|
|
23. |
|
|
|
|
Swap(B[j],
B[leftChild])
// Swap parent and left child |
|
24. |
|
|
|
|
j = leftChild // Move
down to node at the next level |
|
25. |
|
|
|
Else //
Heap property is not violated |
|
|
26. |
|
|
|
|
flag = FALSE |
|
27. |
|
|
|
EndIf |
|
|
28. |
|
|
EndIf |
||
|
29. |
|
EndIf |
|||
|
30. |
EndWhile |
||||
|
31. |
Stop |
||||
So far we have defined the algorithm CreateHeap to create a heap tree for a
given list of elements, the algorithm RemoveMax
to remove the maximum (root element) from a heap tree and the algorithm RebuildHeap to fixing up the heap tree after
removing the element at the root of the heap tree. Now we shall define the
algorithm HeapSort to sort a list of
elements. The basic steps in the heap sort are already discussed and
illustrated in Figure 14.22. The pseudo code of the algorithm HeapSort is given below.
Algorithm HeapSort
Input: An
array A[1, 2, …, n] of n elements.
Output: An
array B[1, 2, …, n] of n elements in
sorted order.
Remark:
Sorting in descending order.
Steps:
|
1. |
Read n elements and stored in
the array A |
|
|
2. |
CreateHeap(A) //
Create the heap tree for the list of elements in A |
|
|
3. |
For i = n down to 2 do
// Repeat n-1 times |
|
|
4. |
|
RemoveMax(B,
i) // Remove
the element at the root and swap it with the i-th |
|
5. |
|
RebuildHeap(B,
i-1) // Rebuild the
heap with the elements B[1, 2, …,
(i-1)], i>1 |
|
6. |
EndFor |
|
|
7. |
Stop |
|
The heap sort technique is illustrated in Figure 14.27
with a list of following 10 elements.
15 35 55 75 05 95 85 65 45 25
It can be verified that the heap tree depends on the
ordering of the elements. That is, for the same list of elements but in
different orders, we get different heap trees. When the sorting is done, the
output list is sorted in asscending order.
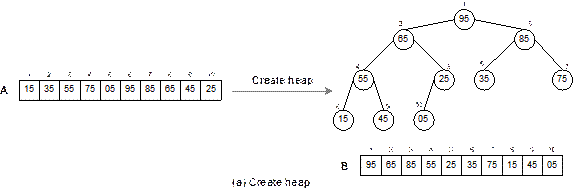

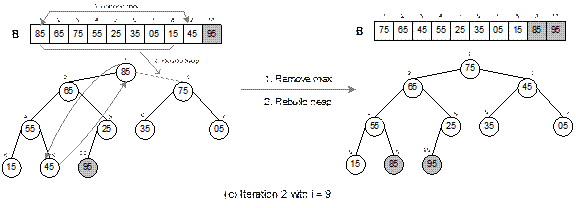
Fig. 14.27 Continued.

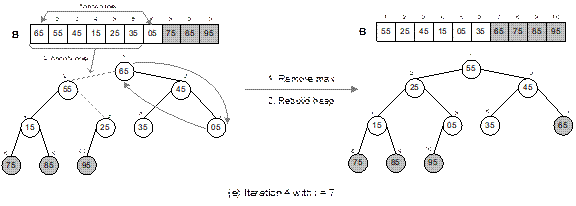
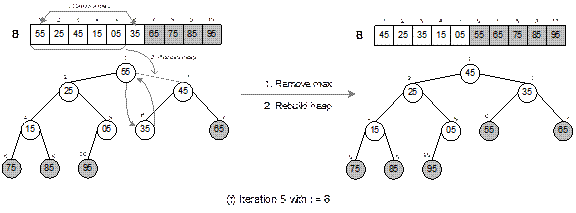
Fig. 14.27 Continued.
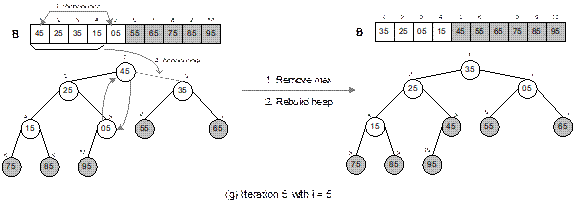

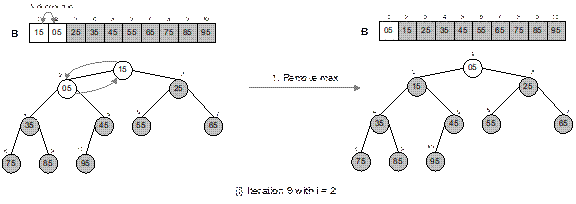
Fig. 14.27 Illustration of heap
sort.
Analysis of the algorithm HeapSort
Let
us analyze the performance of the algorithm HeapSort.
We have learnt that given an input list heap sort produces an output list and
it does not require any extra storage space other than the input list. Let n be the number of elements in the input
list. The storage space required is
![]()
Further, the storage space requirement remains
invariant for any combination of the items provided that number of items
remains same.
Other metrics of the performance of the heap sort,
however, depends on the initial ordering of the elements in the list. In the
following sub sections, we analyze the number of comparisons and number of
movements involved in three different cases of the input pattern.
Case 1: Elements in the input list are in random order
Number of comparisons
There
are three major steps namely, create heap, remove max and rebuild heap. We
analyze the number of comparisons in each and then in sorting method as a
whole.
In create heap
For
n elements, it requires n iterations.
At an iteration i, this method
inserts the i-th element into a heap
of (i-1) elements. To place the i-th elements into its proper place, it
is required to compare with all elements along a path from the node to root
node at the most. In best case, it does not require any comparison. So, the
number of comparisons, in the i-th
iteration varies between 0 and h-1, where h denotes the height of the heap tree in that iteration. We know
that the height of a complete binary tree with i number of nodes in it is given by
![]() (see Lemma 8.6)
(see Lemma 8.6)
Now, the number of comparisons depends on the value
relative to the value of elements in a path from the currently added node to
the root node (see Figure 10.28(a)). In other words, if h be the height of the heap tree and pj is the probability that j number of comparisons is needed, then the average number of
comparisons required will be
= ![]()
If
all elements are distinct and equally probable at any place on the path then,
we have
![]()
With
this assumption, the average number of comparisons in the i-th iteration is
= ![]()
= ![]()
= ![]()
= ![]()
![]()
Considering all iterations from 1 to n, we get the
total number of comparisons C1(n) in the create heap operation,
![]()
To make the calculation simple, let us assume that ![]() . Thus
. Thus
![]() =
= ![]()
In remove max
The
remove max operation, in fact, does not require any key comparison. Hence, we
write for this as
![]()
In rebuild heap
Rebuilding
a heap tree is accomplished by comparing elements starting from the root node
to a leaf node (see Figure 10.28(b)). Let us consider the rebuilding of heap
tree with i number of nodes. The
length of such a path is same as the height of the tree, which is![]() . With the same argument as in case of number of comparisons
while creating heap at an i-th
iteration, here also we can see that the number of comparisons, on the average
is
. With the same argument as in case of number of comparisons
while creating heap at an i-th
iteration, here also we can see that the number of comparisons, on the average
is
= ![]()
= ![]()
![]()
Since,
the rebuild operation is iterated for i
= n to 2, the total number of
comparisons, denoted by C3(n) is given by
![]()
![]()
= ![]()
Total
number of comparisons in the algorithm HeapSort(…), in this case is calculated
as
![]()
= ![]()
= ![]()
Number of movements
Movements
in heap sort come as the swaps of key values. These movements take place in
remove max operation as well as in the create heap and rebuild heap operations.
It can be seen that there are three key movements in a single remove max
operation and the remove max operation iterates n-1 times. Hence, the total number of movements M1(n) due to remove max operation is
![]()
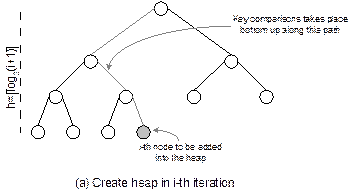

Fig 14.28 Analysis of heap sort
at i-th iteration.
On the other hand, the number of key movements in create
heap and rebuild heap is closely related to the number of key comparisons. For
a comparison there are two possibilities: either swap or no swap. So, it can be
taken as a fair approximation, if we consider the number of movements in these
operations is half of the number of comparisons. Hence, total number of movements in create
heap and rebuild heap operations, denoted by M2(n) is
![]()
So,
total number of movements in heap sort is calculated as
![]()
![]()
Case 2: Elements in the input list are in ascending order
Number of movements
In create heap
When
items in the input list are present in random order, it may not trace entire
path starting from leaf node to root node bottom up. In other hand, when items
in the input list are in ascending order it is required to trace the complete
path starting from a leaf node to the root node. So, at the i-th iteration of the create heap
procedure, the number of comparisons is same as the height but 1 of the heap
tree. To create the heap with n
elements, total number of comparisons is
C1(n) = ![]()
In remove max
Like
Case 1, in this case also, no comparison is involved for this operation. Hence,
C2(n)
= 0
In rebuild heap
Arguing
similarly as in Case 1 and in the calculation of number of comparisons in Case
2, we may write
C3(n) = ![]()
Hence, the total number of comparisons
altogether in the entire heap sort operation is,
![]()
= ![]()
= ![]()
Number of movements
Following
the same argument as in the number of movements calculations in Case 1, we have
Number
of movements in remove max, M1(n)
= 3(n-1)
Number
of movements in create heap and rebuild heap, M2(n) = ![]() =
= ![]()
Therefore,
total number movement is give by
M(n) = M1(n) + M2(n)
=
3(n-1) + log2(n+1)!
Case 3: Elements in the input list are in descending order
Number of comparisons
In create heap
When
items in the input list are in descending order, and an element is added at an i-th stage of building heap, we need
only a single comparison. This is true for all i =1 to n. Hence, the
total number of comparisons in this operation is
C1(n)
= n
In remove max
Same
as in the earlier case, in this case also no comparison is involved. That is,
C2(n)
= 0
In rebuild heap
When
items in the input list are in descending order, the heap at any stage of the
operation has the following characteristics for any two adjacent levels: all
elements in l-th level are greater
that the elements in l+1-th levels.
So, remove max operation eventually moves the smallest element in the heap to
root and in order to rebuild, it is
required to trace the complete path starting from a root node to the leaf node.
So, at the i-th iteration of the
rebuild heap procedure, the number of comparisons is same as the height but 1
of the heap tree. To rebuild the heap with n
elements, total number of comparisons is
C3(n)
= log2(n+1)!
Total
number of comparisons, including all the above operations, we have
C(n) = C1(n)
+ C2(n) + C3(n)
= ![]()
= ![]()
Number of movements
When
items in the input list are in descending order, and to add an item at an i-th stage of building heap, we need a
single comparison but don’t need any swap operation. This is true for all i =1 to n. This is unlike the previous two cases. However,
number of movements in remove max operation is same as in the previous two
cases. Further, unlike the previous two
cases, the number of movements in rebuild operation is same as the number of
comparisons. Hence, we may summarize the
number of movements as follows.
Number
of movements in create heap operation, M1(n)
= 0
Number
of movement in remove max operations = M2(n)
= 3(n-1)
Number
of movements in create heap operation, M3(n)
= C3(n) = log2(n+1)!
Therefore,
total number of movements is
M(n) = M1(n)
+ M2(n) + M3(n)
= 3(n-1) + log2(n+1)!
From the analysis of the algorithm HeapSort, we can summarize the results
as shown in Table 14.12.
Table 14.12 Analysis of the algorithm HeapSort.
|
Case |
Comparisons |
Movement |
Memory |
Remark |
|
Case 1 |
|
|
|
Input list is in sorted
order |
|
Case 2 |
|
|
|
Input list is sorted in
reversed order |
|
Case 3 |
|
|
|
Input list is in random
order |
The
run time complexity T(n) of the
algorithm HeapSort can be calculated considering the number of comparisons and
number of movements, that is,
![]() .
.
Assuming t1
= t2 = c, where c ≥ 0 is a constant, and Starling’s approximation formula
that ![]() (see Appendix A), the
run time complexity of the algorithm for three different patterns of the input
list is shown in Table 14.13.
(see Appendix A), the
run time complexity of the algorithm for three different patterns of the input
list is shown in Table 14.13.
Table 14.13 Time complexity of the algorithm HeapSort.
|
Case |
Run time, T(n) |
Complexity |
Remark |
|
Case 1 |
|
|
Best case |
|
Case 2 |
|
|
Best case |
|
Case 3 |
|
|
Worst case |
Note: From the analysis of the heap sort, it is evident that so far the
number of comparisons is concerned, heap sort performs worst when the elements
are sorted but in reversed order. In other words, it performs better when the
elements are in random order. It also shows best performance when the elements
in the input list are already in sorted order.
SORTING BY EXCHANGE
In
this section, we shall discuss another set of sorting techniques, which are
based on the principle of “sorting by exchange”. The basic concept in this technique
is to interchange (exchange) pairs of elements that are out of order until no
more such pair exists. Following are the sorting techniques based on this
principle and included in our subsequent discussion.
·
Bubble sort
·
Quick sort
All these sorting techniques
are discussed in the following sub sections.
Bubble Sort
This
is the simplest sorting technique among all the sorting techniques known. This technique
is simple in the sense that it is easy to understand, easy to implement and
easy to analyze. The working of the bubble sort is stated below.
Let
us consider that n elements to be
sorted are stored in an array.
- While location of the
first element is not same as the location of the last element do Step 2-7.
- Let’s start with the first element
as the current element.
- While current element is not the
same as the last element repeat Step 4-6.
- Compare the current element with
the immediate next element.
- If the two elements are
not in order then swap the two.
- Move to the next element,
and it is now the current element.
- The largest element is now placed
at its right location. The element just
ahead to this
element becomes the last element of the rest of the unsorted list. Go to
Step 1.
- Stop.
From the above description of the bubble sort, we see
that it consists of two loops: outer loop (Step 1-7) and inner loop (Step 3-6).
For each execution of the outer loop, an inner loop is executed. To sort n number of elements, the outer loop is
executed n-1 times. The first outer
loop rolls the inner loop n-1 times,
the second outer loop rolls the inner loop n-2
and so on. After the iteration of outer loop n-1 times, all elements are placed in their places according to a
sorted order.
The bubble sort derives its name from the fact that
the smaller data items “bubble up” to the top of the list. This method is also alternatively termed as
“sinking sort” because larger elements “sink down” to the bottom (see Figure 14.30).
For example, in the first pass of the outer loop, the largest key in the list
moves to the end. Thus, the first pass assures that the list will have the
largest elements at the last location. The same operation is to be repeated for
remaining n-1 elements other than
this largest element, so that the second largest element is placed in its
position. Repeating the process for a total of (n-1) passes will eventually guarantee that all items are placed in
sorted order. The following algorithm
bubble sort makes this informal description of the method precise.
Algorithm BubbleSort
Input: An array A[1,2, ..., n], where n is the number
of elements.
Output: Array A with all elements in sorted order.
Remark: Sort the
elements in ascending order.
Steps:
|
1. |
For i =1
to n-1 do
// Outer loop with n-1 passes |
|||
|
2. |
|
For j = 1
to n-i do
// Inner loop: in the i-th pass |
||
|
3. |
|
|
If (A[j]
> A[j+1] ) then // Check if two elements are out of order |
|
|
4. |
|
|
|
Swap(A[j], A[j+1])
// Interchange A[j] and A[j+1] |
|
5. |
|
|
EndIf |
|
|
6. |
|
|
j = j + 1
// Move to the next elements |
|
|
7. |
|
EndFor |
||
|
8. |
EndFor |
|||
|
9. |
Stop |
|||
Fig. 14.30 The principle of the bubble sort.
Illustration of the
algorithm BubbleSort
Figure
14.31 illustrates the algorithm BubbleSort with an input list A with 8 elements
sorted in it. Figure 14.31 shows 7 passes. Exchanges of data in each pass are
summarized. Readers are advised to verify by tracing the algorithm.

Fig 14.31 Illustration of the
BubbleSort Algorithm.
Analysis
of the algorithm BubbleSort
In
this sub section, we analyze the number of comparisons, movements, storage
spaces required for the algorithm BubbleSort. Let us first consider the storage
space requirements. From the illustration of the bubble sort technique, it is
evident that the bubble sort algorithm does not require any additional storage space
other than the list itself. In other words, bubble sort works with the same as
the input array. Hence, the algorithm BubbleSort is an in place sorting method. Therefore, if n elements are there in the input list,
then additional storage space requirement is
S(n) = 0
The
storage space requirement is irrespective of the ordering of the elements in
the input list. Number of comparisons and number of movements, on the other
hand, depends on the ordering of the elements.
We analyze these two metrics for the following three cases.
Case 1: The input list is already in sorted order
Number of comparisons
Let
us consider the case of the i-th
pass, where ![]() . In i-th pass, i-1
elements are already sorted (see Fig. 10.30) and inner loop iterates comparing
with 1 to n-(i-1)-1 elements. Hence, total number of key comparisons in the i-th
pass is =
. In i-th pass, i-1
elements are already sorted (see Fig. 10.30) and inner loop iterates comparing
with 1 to n-(i-1)-1 elements. Hence, total number of key comparisons in the i-th
pass is = ![]() . Considering all passes, total number of comparisons is
. Considering all passes, total number of comparisons is
![]() =
= ![]()
![]()
Number of movements
In
this case, no data swap operation takes place in any pass. Hence, number of
movement M(n) is:
M (n) = 0
Case 2: The input list is sorted but in reversed
order
Number of comparisons
Number
of comparisons in this case is same as in the case 1. Hence, we have
![]()
Number of movements
In
this case the comparison in Step 3 is always true. Hence, the number of
movements is same as the number of comparisons. That is, in i-th iteration of the algorithm, number
of movement is n-i. Therefore, total number of key movements is
![]() =
= ![]()
![]()
Case 3: Elements in the input list are in random order
Number of comparisons
Like
the previous two cases, in this case also all iterations in outer loop as well
as in inner loop occur. Hence, number of comparisons involved in this case
remains same as in the previous two cases. Therefore, the total number of
comparisons is
![]()
Number of movements
To
calculate the number of movements in this case, let us consider the i-th
pass of the algorithm. We know that in the i-th
(1≤ i≤ n-1) pass, (i-1) elements are present in sorted part (bottom part) and (n-i+1)
elements are in unsorted part (top) in the array. We are to calculate the
number of swap operations on the average that may occur in this pass. Let pj be the
probability that the largest element is in the unsorted part is in j-th (1≤j≤n-i+1) location.
If the largest element is in the j-th
location then the expected number of swap operation is ![]() . Therefore, the average number of swaps in the i-th pass is given by
. Therefore, the average number of swaps in the i-th pass is given by
![]()
To simplify the above calculation, assume that largest
element is equally probable at any place and hence,
![]() =
= ![]()
With
the assumption, the average number of swaps in the i-th
pass stands as
![]()
= ![]()
= ![]()
= ![]()
Consider
all the passes between i =1 to n-1, the average number of movements, M(n)
is given by
![]()
= ![]()
From
the analysis of the algorithm BubbleSort, we summarize the results as
shown in Table 14.15.
Table 10.15 Analysis of the algorithm BubbleSort.
|
Case |
Comparisons |
Movement |
Memory |
Remark |
|
Case 1 |
|
|
|
Input list is in sorted
order |
|
Case 2 |
|
|
|
Input list is sorted in reversed
order |
|
Case 3 |
|
|
|
Input list is in random
order |
The
time complexity T(n) of the algorithm
BubbleSort can be calculated considering the number of comparisons and
number of movements, that is,
![]()
where
t1 and t2 denote the time
required for a unit comparison and movement, respectively. The time complexity
is summarized in Table 10.16 assuming![]() , where c is a
constant.
, where c is a
constant.
Table 14.16 Time complexity of the algorithm BubbleSort.
|
Run time, T(n) |
Complexity |
Remark |
|
|
|
Best case |
|
|
|
Worst case |
|
|
|
Average case |
Note: From the above analysis, we observe that the best
case of the BubbleSort algorithm occurs when the list is already in
sorted order, worst case occurs when the list is sorted but in reversed order
and average case occurs when the elements in the list are in random order.
Refinements in the Bubble
Sort
The
bubble sort technique that we have discussed in the last section is a simple
approach and it performs some operations which could be avoided so that it then
run faster. Several refinements can be thought in order to improve the
performance of the bubble sort. Two such refinement strategies are discussed in
the following.
Refinement 1: Funnel sort
The
present version of the bubble sort algorithm requires n(n-1)/2 comparisons to
sort a list irrespective of the ordering of the elements in the list. Suppose
the list is already in sorted order or almost sorted (few elements are away
from their final positions). In such a situation, it happens that majority of
the passes are routinely rolled. We can refine the bubble sort method to avoid
such a situation. A single Boolean variable is enough to control this spurious
passes. This Boolean variable signals the end of the sorting operation when no
interchange takes place during the just finished pass. The modified version of
the bubble sort is termed as funnel sort. The following algorithm FunnelSort is designed to take into
account the above.
Algorithm FunnelSort
Input: An array A[1,2, ..., n], where n is the number
of elements.
Output: Array A with all elements in sorted order.
Remark: Sort the
elements in ascending order.
Steps:
|
1. |
flag = TRUE // The
Boolean variable to control the outer loop, initially TRUE |
|||
|
2. |
i = 1
//
To count the number of outer loop |
|||
|
3. |
While(flag = TRUE and i < n ) do
// Outer loop with n-1 passes |
|||
|
4. |
|
flag = FALSE //
Reset the Boolean variable |
||
|
5. |
|
For j = 1 to n-i do
// Inner loop: in the i-th pass |
||
|
6. |
|
|
If (A[j] > A[j+1] ) then // Check if two elements are
out of order |
|
|
7. |
|
|
|
Swap(A[j],
A[j+1])
// Interchange A[j] and A[j+1] |
|
8. |
|
|
|
flag = TRUE
// Reset the Boolean variable |
|
9. |
|
|
EndIf |
|
|
10. |
|
|
j = j + 1
// Move to the next elements |
|
|
11. |
|
EndFor |
||
|
12. |
|
i = i + 1 |
||
|
13. |
EndWhile |
|||
|
14. |
Stop |
|||
Explanation of the
algorithm FunnelSort
A
Boolean variable flag is used and
initialized as TRUE (in Step 1) and it implies that the pass is to be
continued. Another variable i is defined and initialized to 1, which
counts the number of outer loop the algorithm goes through. Like the algorithm BubbleSort,
in the FunnelSort algorithm also two loops are there: outer lop (Step
3-13) and inner loop (Step 5-11). The outer loop begins with setting the
Boolean variable flag = FALSE to
indicate that possibly no interchange is required. If there is no interchange then
it remains FALSE and thus breaking the outer loop. Otherwise, the flag is set
to TRUE and the next outer loop is executed or algorithm terminates if the n-1 outer loops are done.
Refinement
2: Cocktail sort
It
may be noticed that in the algorithm BubbleSort, the largest element sinks down more
than one steps per pass but the smallest element bubble up one move only, that
is, one step per pass; so if the smallest element happens to be initially at
the far bottom, we are forced to make the maximum number of passes. This
situation better can be explained with an example, which is shown in Fig. 14.32. In Fig 14.32, we see that the largest element
96 moves from top to bottom in the first pass itself whereas the smallest
element destine to the top location reaches only at the last pass. This
limitation in the bubble sort can be alleviated by making alternative passes go
in opposite directions: that is during passes from top to bottom moving the
largest towards the bottom and during the passes from bottom to top moving the
smallest element towards the top. This refinement is illustrated in Fig. 14.33.
Based on the above discussion another refined version
of the bubble sort method entitles “cocktail sort” is proposed, which is
precisely defined in the algorithm CocktailSort.

Fig 14.32 Slow bubbling of
smallest element.
Algorithm CocktailSort
Input: An array A[1,2, ..., n], where n is the number
of elements.
Output: Array A with all elements in sorted order.
Remark: Sort the elements
in ascending order.
Steps:
|
1. |
flag = TRUE // The Boolean
variable to control the outer loop, initially TRUE |
||||
|
2. |
top = 1, bottom = n
// Tracker to locate top and bottom locations |
||||
|
3. |
passNo = 1
// Counts outer loop |
||||
|
4. |
While(flag = TRUE and top < bottom ) do
// Checking for outer loop |
||||
|
5. |
|
flag = FALSE
// Reset the Boolean variable |
|||
|
6. |
|
If (passNo mod 2 = 1) then //
Pass for moving from top to bottom |
|||
|
7. |
|
|
For j = top to
bottom-1 do //
Inner loop: in the current pass |
||
|
8. |
|
|
|
If (A[j] > A[j+1] ) then // Check if two
elements are out of order |
|
|
9. |
|
|
|
|
Swap(A[j],
A[j+1])
// Interchange A[j] and A[j+1] |
|
10. |
|
|
|
|
flag = TRUE
// Reset the Boolean variable |
|
11. |
|
|
|
EndIf |
|
|
12. |
|
|
EndFor |
||
|
13. |
|
|
bottom = bottom -1 // Current largest element is
now in sorted part (bottom) |
||
|
14. |
|
Else //
Pass for moving from bottom to top |
|||
|
15. |
|
|
For j = bottom down to top + 1 do // Inner loop: in
the current pass |
||
|
16. |
|
|
|
If (A[j] <
A[j-1] ) then // Check if two elements
are out of order |
|
|
17. |
|
|
|
|
Swap(A[j],
A[j+1])
// Interchange A[j] and A[j+1] |
|
18. |
|
|
|
|
flag = TRUE
// Reset the Boolean variable |
|
19. |
|
|
|
EndIf |
|
|
20. |
|
|
EndFor |
||
|
21. |
|
|
top = top + 1 // Current
smallest element is now in sorted part (top) |
||
|
22. |
|
EndIf |
|||
|
23. |
|
passNo = passNo + 1
// Next consider for the next pass |
|||
|
24. |
EndWhile |
||||
|
25. |
Stop |
||||
Explanation of the
algorithm CocktailSort
The
algorithm cocktail sort in fact is a cocktail (hence the name) of two
refinements over the algorithm bubble sort. Like the bubble sort, we consider
forward pass and like the funnel sort, the Boolean variable flag is used to control the outer loop.
Extra thing in the cocktail sort is the backward pass in addition to the
forward pass. It can be observed that in the cocktail sort, sorted part grow
from the both ends unlike the previous two methods, where the sorted part grows
from the bottom end only. The cocktail sort is illustrated in Figure 14.33. The
arrows in Figure 14.33 show the direction of passes. We see that at the pass 6,
the execution is terminated because in that pass there is no interchange and
hence the control variable flag
becomes false.
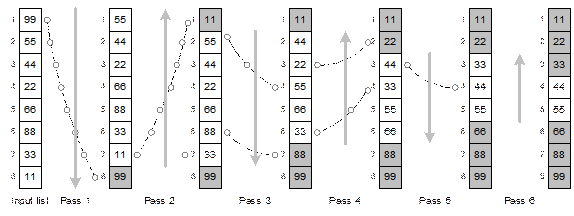
Fig 14.33 Illustration of the
cocktail sort.
Quick Sort
Even
though the shell sort provides a significant advantage in run time over its O(n2) predecessors, its
average efficiency O(nr) with 1<r<2 may still not be good enough for a list with large number of
elements. The next sorting method we will study is called quick sort developed by C. A. R. Hoare in 1962, have an average run
time of O(nlog2n) and treated as a better sorting
method, particularly for sorting a large task.
From the sorting methods studied so far, we can draw a
conclusion that sorting a smaller list with any one of these methods is faster
than a larger list (for example, if the number of elements in the list is
doubled, sorting time increases quadratically). Hence, a way may be thought of
as dividing a large list into a number of smaller lists, sort them separately
and then combine the results to get the original list sorted. C. A. R. Hoare
adopted this divide-and-conquer
approach in his novel work “quick sort” published in Computer Journal, Vol. 5,
No. 1, Pages 10-15, 1962. Let’s first discuss the basic principle of
divide-and-conquer strategy and then its adaptation in quick sort method.
Divide and conquer
The
principle of divide and conquer strategy is to solve a large problem by solving
the smaller instances of the problem. It has three basic steps and is illustrated
in Figure 10.35. Three basic steps are: divide, conquer and combine. We explain
each of these steps below.
Divide:
Divide the large problem to a
number of smaller sub problems. If the sub problems are not small enough then
decompose them and continue the decomposition until all sub problems are small
enough. Let the main problem is divided
into n number of sub problems after
this step and these are P1,
P2, P3, …, Pn. (see Figure 10.35).
Conquer:
Find a suitable technique so
that
each sub problem Pi,
i = 1, 2, 3, …, n can be solved quickly.
Combine: Combine the results of all solutions to all sub
problems to get the final solution.
We learnt that in the divide and conquer strategy
three tasks are there. Now the questions that arise are: How to divide a large
problem into smaller problems? How to solve a smaller problem? How solutions
for all smaller problems can be combined into a final solution? Let us try to answer
these questions.

Fig. 14.35 Divide and conquer
strategy.
In general, a recursive procedure is followed to
achieve these tasks. The recursive framework of divide-and-conquer approach can
be stated as below.
Divide-and-Conquer(P) // P is a
problem to be solved
1. n
= Size(P) // n denotes the
size of the problem
2. If (n
≤ MIN) // MIN denotes the desirable
minimum size of a sub problem and also
// the termination condition
S = Conquer(P) //
Solve the smallest unit using a simple method
3. Else {P1,P2, P3, ..., Pn}
= Divide(P) // Divide P
into n sub problems
4. For each Pi ![]() {P1, P2, ..., Pn} do
{P1, P2, ..., Pn} do
Si =Divide-and-Conquer(Pi)
// Call recursively
5. S
= Combine(S1,S2,
…, Sn) // Combine all
solutions
6. Return(S)
In this framework, three subroutines, Divide, Conquer and Combine are
used, which are in fact problem specific. In this book, we will learn about
these sub routines in two sorting methods, namely, quick sort and merge sort
(in Section 10.7.3) and one searching method namely, binary search method (in
Section 11.3.2). In the present section, we deal with the quick sort only.
Divide-and-conquer approach in quick sort
Let
A[1, 2, …., n] be a list of n
elements to be sorted. The three steps of divide-and-conquer in the context of
quick sort are illustrated in Figure 10.36 and also described as follows.
Divide: Partition the list A[1, 2, …, n] into two
(possibly empty) sub lists A[1, .... p-1] (left sub list) and A[p+1,
..., n] (right sub list) such that each elements in the sub list A[1,
..., p-1] is less than or equal to A[p]
and each element in the sub list A[p+1, ..., n] is greater than A[p].
In other words, satisfying the above mentioned constraint a partition method
should compute an index p, which in
fact divides the list into two sub lists.
Conquer: Sort the two sub lists A[1, .... p-1] and A[p+1,
..., n] recursively, as if each sub list is a list to be sorted and following
the same divide-and-conquer strategy until the sub lists contain either zero or
one element. This is the desirable minimum size of a sub list to stop further
recursion.
Combine: Since the sub lists are sorted in place, no work is
needed to combine them. That is, the task combine in the quick sort is
implicit.
The
pseudo code for recursively defining the quick sort is very simple and is given
below.
QuickSort(A, first, last)
// A is the array, first
and last denotes the boundaries of the list under sort
1. If
(first < last) then //
This is the termination condition
2. p = Partition(A,
first, last) //
Partition the list at p
3. QuickSort
(A, first, p-1) //
Recursively call for the left sub list
4. QuickSort(A,
p+1, last) //
Recursively call for the right sub list
5. Return
From the above mentioned steps in quick sort, it is
evident that the quick sort technique turns into the partition problem. We
discuss the partition technique in the following.
Partition method in quick sort
Let
the input list is stored in an array A
and l and r are the two pointers pointing the left most and right most
elements in the list. We shall select any element in the list as pivot element
and partition method will place the pivot element in a location loc such that any element at the left
side of loc is smaller than the pivot
element and any element at the right side of loc is greater than the pivot element. There are several methods to
select an element as the pivot element. Here, we will follow the simple one,
that is, left most element as the pivot element (see Fig. 14.37(a)). To find
the final position of the pivot element we perform two scans: scan from right
to left and scan from left to right. While scanning from right to left, the
pivot element is at the location l
and we are comparing the element at r
and move from right to left until the element currently at r is greater than the pivot element (Figure 14.37(b)). On the other
hand, while scanning from left to right, the pivot element is at the location r and we compare the element at l until the element currently at r is less than the pivot element.
Scanning halts whenever the condition breaks and is followed by an interchange.
These two scans are repeated until the entire list is scanned, that is, l ≤ r. At the end of the partition method, the pivot element is placed
in its final position according to sorting order (see Figure 14.37(c)). Note
that loc points the current location
of the pivot element and changes in the pointers l and r, after a scan is
over. The following algorithm makes this informal description of the partition
method precise.

Fig. 14.36 Divide-and-conquer in
quick sort.

(a)
List
under partition (initial)

(b)
Scan
from right to left
Fig. 14.37 Continued.

(c)
Scan
from left to right
Fig. 14.37 Illustration of the partition method.
Algorithm Partition
Input: A list of elements stored in an array A. The left most and right most elements
of the list under
partition are located at left and right, respectively.
Output: Returns
loc as the final position of the
pivot element.
Remark: The
element located at left is taken as
the pivot element.
Steps:
|
1. |
loc = left /
/ The left most element is chosen as the pivot element |
|||
|
2. |
While ((left
< right) do
// Repeat until the entire list is scanned |
|||
|
3. |
|
While(A[loc]
≤ A[right]) and (loc <
right) do // Scan
from right to left |
||
|
4. |
|
|
right = right -1 //
No interchange. Move from left to right |
|
|
5. |
|
EndWhile |
||
|
6. |
|
If (A[loc]
> A[right]) then |
||
|
7. |
|
|
Swap(A[loc],
A[right]) //
Interchange the pivot and the element at right |
|
|
8. |
|
|
loc = right
// The pivot is not at the location right |
|
|
9. |
|
|
left = left +1 // Next scan
(left to right) begins from this location |
|
|
10. |
|
EndIf |
||
|
11. |
|
While(A[loc]
≥ A[left]) and (loc > left)
do // Scan from left to right |
||
|
12. |
|
|
left = left +1
// No interchange. Move from right to left |
|
|
13. |
|
EndWhile |
||
|
14. |
|
If (A[loc]
< A[left]) then |
||
|
15. |
|
|
Swap(A[loc],A[left]) // Interchange
the pivot and the element at left |
|
|
16. |
|
|
loc = left
// The pivot is not at the location left |
|
|
17. |
|
|
right = right-1 // Next
scan (right to left) begins from this location |
|
|
18. |
|
EndIf |
||
|
19. |
EndWhile |
|||
|
20. |
Return (loc) |
|||
|
21. |
Stop |
|||
Illustration of the
partition method
Let
us consider a list of elements stored in an array A = [55, 88, 22, 99, 44, 11,
66, 77, 33]. We want to partition the list A
into two sub lists. Different situation of the algorithm Partition is illustrated in Figure 14.38.
Here, left =
1 and right = 9 are the pointers to
the left most and right most element, respectively. Further, the left most
element, that is, 55 is selected as the pivot element. The current location of
the pivot is loc, which is same as
the left most pointer left (Step 1)
and shown in Figure 14.38(a).
Next step is to scan from right to left while pivot
element is at left. The while-loop in
Step 3-5 takes care of this and the result on execution of this loop is shown
in Figure 14.38(b). We see the break of the loop since 55 > 33 and
subsequently followed by a swapping of 55 and 33 according to the Steps 5-10.
Since, the if-condition at Step 11 is not satisfied, the next step is to scan
from left to right while the pivot element is at right (here at 9, see Figure 14.38(b)).
The condition of while-loop (Step 14-16) does not satisfy. Hence, immediate
steps viz. Step 17-21 is followed and outcome is shown in Figure 14.38(c). This
completes one execution of the outermost loop, that is, Step 2-25. At the
beginning of the next iteration of this loop, the condition of the outermost
while-loop is checked (Step-2) and loop condition is satisfies. Scan from right
to left begins at Step 3. The while-loop (Step 3-5) is executed for two
iterations and then the if-statement (Step 6-10) is executed whose result is
shown in Figure 14.38(d). Next , the condition in if-statement (Step 11) fails
and scan from left to right begins at Step 12, the result of this scan
(according to Step 14-16 and subsequently, it follows the Step 17-21). The
if-statement at Step 22 still fails and control goes to the outermost loop
(Step 2). At the beginning of the third iteration of the outermost loop, scanning
stats from right to left but the while statement (at Step 3 ) is checked and
condition for execution fails. Next, the condition of if-statement (Step 6) is
found true and Steps 6-10 are executed, the result of which is shown in Figure
14.38(e). Finally, the condition of if-statement (Step 11) becomes true and the
algorithm stops its execution by returning the location of the pivot element.


Fig. 14.38
Continued.



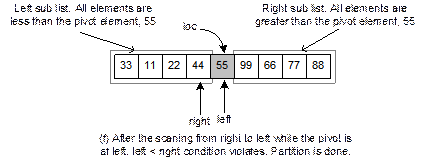
Fig. 14.38 Illustration of the algorithm Partition.
Hoare’s
partition method
The
partition method discussed above is not due to Hoare. Here is the partition
algorithm originally proposed by Hoare in his quick sort technique.
Algorithm HoarePartition
Input: An array A[l….r],
l and r being the left and right most pointers in the list, respectively
Output: loc being
the location of splitting point in the array.
Remark:
The element at the l-th location is
chosen as the pivot element.
Steps:
|
1. |
pivot = A[l]
// The left most element is chosen as the pivot element |
||
|
2. |
low = l-1, high = r // Two pointer to
indicate two extreme ends and initialized here |
||
|
3. |
Do
// Outer loop continues for entire scan |
||
|
4. |
|
Do
// Scan from right to left |
|
|
5. |
|
|
high = high -1 |
|
6. |
|
While
(pivot ≤ A[high]) and (low < high) |
|
|
7. |
|
Do
// Scan from left to right |
|
|
8. |
|
|
low = low + 1 |
|
9. |
|
While
(pivot ≥ A[low]) and (low < high). |
|
|
10. |
|
Swap (A[low],
A[high]) // Pair of
entries are swapped as they are in the wrong sides |
|
|
11. |
While (low
< high) do
// Outer loop until entire list
is sacnned |
||
|
12. |
loc = low // This is
the location of the pivot and it is in its final place |
||
|
13. |
Swap
(A[loc], A[l]) |
||
|
14. |
Return
(loc)
// Return the location of the pivot |
||
|
15. |
Stop |
||
Explanation of the
Hoare’s partition method
Two
pointers low and high are maintained such that all elements before the position low are less than or equal to the pivot
element and all elements after the position high
are greater than or equal to the pivot elements. The idea in the Hoare’s method
is to use two pointers moving from the two ends of the list towards the center
(or actually a split position) and perform a swap only when a large element is
found by the low position and a small
element by the high position. These
movements are controlled by the two inner Do-While loops (Step 4-6 and Step
7-9) in succession. Each of these loops is controlled by two checks (Step 6 and
Step 9), with two predicates: the first is to check the invariant property and
the second to ensure that the pointer does not go out of the range. When a pair
of entries, each on the wrong side is found then they should be swapped (in
Step 10) and the loops are repeated under the control of an outer loop (Step
3-11). The outer loop is terminated when the pointers go out of range, that is,
low ≥ high. At the termination of the outer loop, either pointer
indicates the position of split. Note that pivot remains at the left most end l. At the end, the pivot is swapped with
the element at the split position, that is, pivot is placed into its proper
place (Step 13). Finally, it returns the final position of the pivot element
(Step 14).
Algorithm for Quick sort
Now,
we are in a portion to have a precise definition of the quick sort technique,
which is defined through a recursive algorithm QuickSort.
Algorithm QuickSort
Input: A list of elements stored in an array A[low…high], where low and high
are the two boundaries.
Output: Elements in A are stored in ascending order.
Remarks: Algorithm is defined recursively.
Steps:
|
1. |
Loc = Partition(left, right)
// left and right are two pointers to locate
partitions
// at left and right,
respectively |
|
|
2. |
If (left
< right) then
// Check for the termination condition |
|
|
3. |
|
QuickSort(A,
left, loc-1)
// Perform quick sort
over the left sub list |
|
4. |
|
QuickSort(A,
loc+1, right) /
Perform quick sort over the right sub-list |
|
5. |
EndIf |
|
|
6. |
Stop |
|
Illustration of the algorithm QuickSort
We
can trace the algorithm QuickSort
with the following list as a sample.
55 88 22 99 44 11 66 77 33
The
execution according to the algorithm QuickSort
is illustrated as a recursion tree
shown in Figure 10.39. The recursion tree explains how the call of different
subroutine in the QuickSort algorithm
occurs for a given list as input. A recursive call of QuickSort is denoted by ↓ as shown in Figure 10.39. At every
node in the recursion tree, partition method is called followed by two
recursive calls of QuickSort on the
left and right sub lists (obtained as a result of partition method). The pivot
element is placed at the node and the left sub-tree and right sub-tree are
expanded recursively. It is interesting to note that, if we visit the recursion
tree in inorder traversal then the
order of visiting elements is same as the ascending order of elements.
Fig. 14.39 Illustration of the
algorithm QuickSort.
Analysis of the
algorithm QuickSort
Let
us analyze the performance of the QuickSort
algorithm from storage, movement, and time requirements point of views.
Memory requirement
From
the illustration of the quick sort method, it appears that it is an in place
sort. In fact, quick sort is not an in place sorting method! This is because,
after one partition is over, it produces two sub lists (possibly empty) and
same method is required to be repeated either iteratively or recursively.
Whatever is the procedure, it is always necessary to maintain a stack. Why a
stack is required? An answer to this question can be had from Section 4.5.5
where it has been thoroughly explained the application of stack in the
implementation of quick sort. We recall that, a stack is required to store all
sub lists (nothing but the two boundary indexes of the lists) which are yet to
be processed. Initially, the stack is pushed with the two boundary indexes of
the input list and first recursion starts with the call to this list. On
partition, it produces two sub lists, which are pushed onto the stack. It then
pops a list, call quick sort on the list popped, pushes two lists on partition
and so on. These steps are repeated until the stack is empty. It is evident
that the size of this stack depends on the number of sub lists into which a
list may be partitioned towards the completion of the sorting. Now, every call
makes one pop and two pushes, thereby net increase in stack entry is one. In
other words, size of the stack should be as large as the number of recursive
calls involved. Number of recursive calls, however, depends on how the lists
are partitioned during recursions. It can be analyzed that least number of
recursive calls occurs when each recursion splits a list into two (nearly)
equal halves. In such a case maximum size of the stack would be ![]() +1, where n is
number of elements in the input list (see Figure 14.40(a)). In other hand, if
the input list is either sorted in ascending or descending order then the
number of recursive call will be exactly n
(by Lemma 10.1 and see Figure 14.40(b)). In this case, there will be at most
one entry in the stack. This is because one sub list will be always empty, and
it pushes the non-empty sub list, which popped in the next recursion and this
continues till there is a single element in the non-empty sub list. So,
considering the worst case situation, the storage space requirement S(n)
to sort a list with n elements is
+1, where n is
number of elements in the input list (see Figure 14.40(a)). In other hand, if
the input list is either sorted in ascending or descending order then the
number of recursive call will be exactly n
(by Lemma 10.1 and see Figure 14.40(b)). In this case, there will be at most
one entry in the stack. This is because one sub list will be always empty, and
it pushes the non-empty sub list, which popped in the next recursion and this
continues till there is a single element in the non-empty sub list. So,
considering the worst case situation, the storage space requirement S(n)
to sort a list with n elements is
![]()
Time complexity
From
the algorithm QuickSort, we can see
that the time complexity of a call of this sorting method is decided by the
partition method and calls of two QuickSort
on two lists of smaller sizes. If T(n) represents total time to sort n
elements and P(n) represents the time for performing partition, then we can write:
T(n) = P(n)
+T(nl) +T(nr) with T(1) = T(0) = 0
where,
nl = number of elements in
the left sub list, nr =
number of elements in the right sub list and 0 ≤ nl, nr
< n.
It can be noted that basic operations in the quick
sort technique is comparison and exchange. Further, quick sort is basically a
repetition of partition methods. Let C(n) and M(n) denote the number of
comparisons and movements, respectively. Then we can write T(n) = C(n)
+ M(n). Number of these two operations required however, depends on the
arrangement of the elements in the input list. There are three major cases of
the input arrangement for which we calculate the time complexities.
Case 1: Elements in the list are stored in ascending order
Number of comparisons
In
this case, the partition method requires only one scan from right to left with n-1 comparisons. In this case, the
partition method results the left sub list as empty and right sub list with n-1 elements. Hence, the recurrence
relations for the number of comparisons can be written as
C(n) = n-1 + C(n-1), with C(1) = C(0) = 0
Expanding
this recurrence relation, we get
![]()
= ![]()
Number of movements
No
exchange operation is involved in this case. Hence, the number of movement M(n)
is given by
M(n) = 0
Case 2: Elements in the list are stored in descending order
Number of comparisons
In
this case, the partition method requires n-1
comparisons. Like in Case 1, the partition method in this case also produces
one empty sub list and other is with n-1
elements. Unlike the Case 1, in this
case the non-empty sub lists are alternatively left sub list and right sub
list. It can be verified that for every odd numbered recursive call, right sub
list is empty, whereas for every even numbered recursive call the left sub list
is empty (see Figure 10.40(b)). Now, if C(n) denotes the number of comparisons in
this case then, we have
C(n) = n-1 + C(n-1), with C(1) = C(0) = 0
Expanding
this recurrence relation, we get
![]()
= ![]()
Number of movements
So
far the number of movement is concerned, it can be checked that there is a
single exchange operation in each odd numbered recursive call and no exchange
operation is involved during any even numbered recursive call. As there are
altogether n number of recursions
(see Lemma 10.1 and Figure 10.40(b)), we have the number of movement as

In other way, the same can be represented as ![]()
Case 3: Elements in the list are stored in random order
Number of comparisons
To
find the final berth of the pivot element, we need (n-1) comparisons in the partition method on a list with n elements. Now, assume that the
partition method finds the i-th
position for the pivot elements and thus it results two sub lists: left sub
list with (i-1) elements and right
sub list with ![]() =
= ![]() elements (see Figure 10.41).
elements (see Figure 10.41).
Fig. 14.41 An instance of partition in QuickSort.
Now, all permutations of elements in these two sub
lists are equally likely. To simplify our calculation, we assume that each
possible position for the pivot element is equally likely. That is, the value
of i has any value between 1 and n with a probability = 1/n. Thus, we can write the recurrence
equation for the number of comparisons in this case as
![]() with C(1) = C(0) = 0
with C(1) = C(0) = 0
The above recurrence relation can be simplified as stated
below. The term C(i-1) varies from C(0) to C(i-1) whereas C(n-i) varies from C(n-1) to C(0) over the entire range of summation
series, that is, i = 1 to n-1. In other words, two terms
contribute the same series. So, we can simplify the recurrence relation in Equation 14.34a as shown below.
![]() for n ≥ 1
for n ≥ 1
This
is the recurrence relation of the algorithm QuickSort
on the number of comparisons, on the average case. We can solve this relation in
Equation 14.34b as shown below.
From
Equation 10.34b, we have
![]()
Replacing
n by n-1, we have ![]()
Now,
![]()
= ![]()
= ![]()
![]()
Or ![]()
Let, ![]() . Then
. Then
![]() , with
, with ![]() (10.34c)
(10.34c)
This
is the simplified version of the recurrence relation and can be sloved just by
simple expansion. On expanding the above recurrence relation, we get
![]()
Finally, ![]()
The first summation is a
harmonic series and whose sum is (see Appendix A, A.6.33) is
![]()
The second summation is given
by
![]() .
.
Hence, we get
![]()
Substituting ![]() in Equation 10.34e, we get
in Equation 10.34e, we get
![]() (10.34f)
(10.34f)
Special case
Let
us analyze a special case that can lead us to an important conclusion. Assume
that elements in the input list are arranged in such a way that every instance
of partition method exactly partitions the list into two lists of equal size.
The recursion relation in this particular case will be given as
![]()
The recurrence relation can
be expanded as shown below.
![]()
= ![]()
= ![]()
= ![]()
For
the sake of simplicity in calculation, let n
= 2k for some k ≥ 0.
Also using C(0) = 0, we get from Equation 10.35b
![]()
= ![]()
= ![]()
= ![]()
![]()
This
is in fact the simplest form of the number of comparisons, usually referred in
the text books and also treated as the best case performance of the quick sort.
Number of movements
We
select the first element as the pivot element in the partition method and it is
equally likely to be placed in any portion in the list. Let the location of the
pivot be i, where 1 ≤ i ≤ n. Then after the partition, the pivot element is guaranteed to be
placed in location i with 1…(i-1) elements in the left sub list and (i+1)…..n elements in the right sub
list (see Figure 10.41). The number of exchanges that is necessary to do this
should not exceed (i-1) for each of (i-1) elements less than the pivot
elements. let us denote M(n), the average number of exchange
operations done by the QuickSort on a
list of size n. Then we have
![]()
Here,
we have taken the average of all number of movements assuming that the pivot may be placed in any location
between 1 and n with a probability =
1/n. Simplifying the recurrence
relation in Equation 10.36a, we get
![]()
Since
this recursion relation is similar to the recurrence relation for the number of
comparisons we have already discussed, the same steps can be followed to solve
for M(n), which then can be obtained as
![]()
The analysis of the algorithm QuickSort is summarized in Table 14.19 and Table 14.20 for ready
reference.
Table 14.19 Analysis of the algorithm QuickSort
|
Case |
Comparisons |
Movement |
Memory |
Remark |
|
Case 1 |
|
|
|
Input list is in sorted
order |
|
Case 2 |
|
|
|
Input list is sorted in
reversed order |
|
Case 3 |
|
|
|
Input list is in random
order |
The
time complexity T(n) of the algorithm
QuickSort can be calculated
considering the number of comparisons and number of movements, that is, ![]() where t1 and
t2 denote the
time required for a unit comparison and movement, respectively. The time
complexity is summarized in the Table 10.20 assuming
where t1 and
t2 denote the
time required for a unit comparison and movement, respectively. The time
complexity is summarized in the Table 10.20 assuming![]() , where c is a
constant.
, where c is a
constant.
Table 14.20 Time complexity of the algorithm QuickSort.
|
Run time, T(n) |
Complexity |
Remark |
|
|
|
Worst case |
|
|
|
Worst case |
|
Or |
|
Best/average case |
Note: In the algorithm QuickSort,
we can see that the partition method decides the fate of the performance of
this sorting method. We have seen that the worst case occurs when the elements
in the list are already in sorting order or in reverse order. The worst case
time complexity is O(n2)
and this is as bad as insertion sort, selection sort or bubble sort algorithms.
Hence, quick sort is nothing but quick when the list is already sorted. A best
case is possible when the partition method always divide the list nicely in equal
halves and in that case, the time complexity is O(nlog2n). We
have also analyzed the average case behavior of the QuickSort, with time complexity
= 4c(n+1)(logen+0.577)-8cn = O(n log2n)
[changing the base in logen
and show that it is ≈ 1.386nlog2n (approximately)]. We therefore can
conclude one fact that the average case complexity of the quick sort is very
close to that of the best case and it is O(nlog2n). Hence, quick sort is quick because
of its average behavior.
Variations in quick sort method
It
is evident that the performance of the quick sort method is directly related to
the performance of the partition method. Further, the performance of the
partition method depends on how the pivot element is selected. The selection of
pivot element may succeed in dividing the list nearly in half (thus yielding
the faster performance) or it may be that one sub list is much larger than the
other (resulting in the slower performance). In our foregoing discussion, we
have chosen the first element as the pivot element. This selection leads to the
method, we may term it is the basic quick sort method. A number of ways the
partition method can be devised and thus providing a number of variations in
the quick sort method. A few important variations are presented in the following
subsections. The performance analyses are left as exercises to the reader.
Randomized quick sort
In
the basic quick sort method, we have always selected the left most element in
the list to be sorted as the pivot element. In randomized quick sort, instead
of using the left most element always, an alternative choice is to choose a
random integer q between l (left most location) and r (right most location), both inclusive
and then select A[q] from the list A[l…..r] as the pivot. This element A[q]
then should be exchanged with A[l] and the rest of the procedure is same
as the basic quick sort method. This modification ensures that the pivot
element is equally likely to be any of the r-l+1 element in the list. Because the
pivot element is randomly chosen, it is expected that the split of the list
would be reasonably in an around the center on the average. The modified
version of the partition method based on the random selection of pivot element
is described below. We term the algorithm as RandomizedPartition.
Algorithm RandomizedRartition
Input: An array A[l….r],
l and r being the left and right most pointers in the list, respectively.
Output: loc being
the location of splitting point in the array.
Remark: The pivot element is chosen at random in between l and r, both inclusive.
Steps:
|
1. |
q = Random(l,
r) //
Generate a random integer in between l and r, both inclusive |
|
2. |
Swap(A[q],
A[l])
// Exchange the two elements between A[q] and A[l]
|
|
3. |
loc = Partition(A, l, r) // Rest of the
things is same as the standard partition method |
|
4. |
Return(loc)
// Return the splitting location |
|
5. |
Stop |
|
Assignment 10.32 |
|
|
Analyze
the running time of the quick sort with the randomized partition method for
the following cases. a) All elements in the input list are
randomly distributed. b) All element in the list are ordered in
ascending order. c) All
element in the list are ordered in descending order. |
|
Random sampling quick sort
An
alternative randomized version of quick sort is to randomize the input by
permutating the given input list. Assume that the input list is in the form of
an array A[1…n]. One common method is to assign each element A[i]
of the list a random priority P[i], and then sort the elements of A according to the priorities. Let us
title this sorting method as random sampling quick sort and is defined below as
the algorithm RandomSampleQuickSort.
Algorithm RandomSampleQuickSort
Input: An array on n elements A[1….n].
Output: All elements are stored in ascending order.
Remark: The list is rearranged.
Steps:
|
1. |
For i =1 to n do |
|
|
2. |
|
P[i]
= Random(1, n3) // Generate a random
number between 1 and n3 |
|
|
|
AssignPriority( P[i], A[i])
// Set i-th random to i-th element |
|
3. |
EndFor |
|
|
4. |
QuickSort(P,1,n) // Call the basic
quick sort on the array P |
|
|
5. |
QuickSort(A, 1, n)
// Call the basic quick sort on the array A |
|
|
6. |
Stop |
|
The basic objective of the algorithm RandomSampleQuickSort is to make the
arrangement of elements in the list random.
To understand the working of the algorithm better, let us consider a
list of four elements. The for-loop Step 1- 4 generates 4 random numbers in the
range 1 to 64 and each of them is associated to an element in the list. It then
sorts the list P using the basic
quick sort. If we consider a structure definition so that an element in A and a random number can be kept
together then sorting over P eventually randomize the elements in
the list. Finally, another call of quick
sort but this time on the list A
produces the list in sorted order. All
the steps mentioned above are illustrated in Figure 10.42.
Input:
A: [ 1 2 3 4]
P: [45 3 63
16] (In for loop: random number generation)
Sorted version of P
P: [ 3 16 45 63] (Step 4)
A: [ 2 4
1
3]
(Random version of A)
Sorted version of A
A: [ 1 2 3 4] (Step 5)
Fig. 14.42 Illustration of the
random sampling quick sort.
Singleton’s
quick sort
R.
C. Singleton in his paper [Communication of the ACM, Vol. 12, pages 185-187,
1969] suggested a way of improvement over the original Hoare’s quick sort method. The Singleton’s approach
was to choose the median of three values A[l],
A[(l+r)/2] and A[r] as the
pivot element in a list A[l….r], where l and r are the left most
and right most indices, respectively.
Multi-partition
quick sort
Instead
of three median as suggested in Singleton’s quick sort method, W. D. Frager and
A. C. McKellar (in the Journal of the ACM Vol. 17, pages 496-497, 1970) have
suggested taking a much larger sample consisting of 2k-1 elements, where k
is chosen so that 2k ≈
n/log2n, n being the size of
the list. The sample can be sorted using the basic quick sort method, and then
inserted each of them among the remaining elements at k-distances apart. In other
words, we partition the input lists into 2k
sub lists, bounded by the elements of the sample. Each sub list so
obtained is then sorted using the usual recursive technique.
Leftist
quick sort
The
basic quick sort algorithm contains two recursive calls to itself. After the
call to partition method, the left sub list is recursively sorted and then the
right sub list is recursively sorted. An alternative to this is to make only
one recursive call. This can be done by using an iteration and call for the
left sub list only. We term this modified version of quick sort method as
leftist quick sort and is defined as the algorithm LeftistQuickSort below.
Algorithm LeftistQuickSort
Input: A list of elements stored in an array A[l….r], where l and r are the left most and right most
indices of the list
Output: All elements are sorted in ascending order
Remark: The list is rearranged.
Steps:
|
1. |
While (l < r) do |
|
|
2. |
|
loc = Partition(A, l, r)
// Find the partition of the list |
|
3. |
|
LeftistQuickSort(A, l, loc-1) //
Call the quick sort on the left sub list |
|
4. |
|
l = loc + 1
// Left most index for right sub list |
|
5. |
EndWhile |
|
|
6. |
Stop |
|
From the algorithm LeftistQuickSort,
we see that after the partition method, quick sort is only invoked on the left
sub list. However, the right sub lists are taken into care through the while
loop.
Lomuto’s
quick sort
An
unpublished work of N. Lomuto,
which is attributed by J. L. Bentley in
his book Programming Pearls, Addison-Wesley, Reading MA, 1986, provides a simple and “elegant “ approach of
partitioning a list. The Lomuto’s partition method is illustrated in Figure 14.43.
Assume that the list under partition is in the form of an array. The first
element is selected as the pivot element. The pivot element is shifted to an
auxiliary location keeping its space in the array as window (see Figure 14.43(a)).
The approach is to move the window from left to right such that all elements
smaller than the pivot element are collected at the left side of the window
(left part), all elements greater or equal to the pivot element are collected
immediately at the right side of the window (middle part) and all elements yet
to be examined are at the far right (right part) as shown in Figure 14.43(b).
Initially, the left and middle parts are empty and all unexamined elements are
in the right part. A pointer ptr
points to the first element in the sub list containing unexamined elements
(that is, the right part). This partition method when finds an element at ptr smaller than the pivot element, it
moves that element to the window, then creates a new window one place to the
right by moving a large element from that place to the place pointed by ptr and then ptr advances one step to right until it reaches at the extreme
right end (hence the partition method comes to an end). The pivot from the
auxiliary space is then moved to the window and current position of the window
is returned as loc, the final
position of the pivot element. The above stated partition method is formulated
as the algorithm LomutoPartition
below.
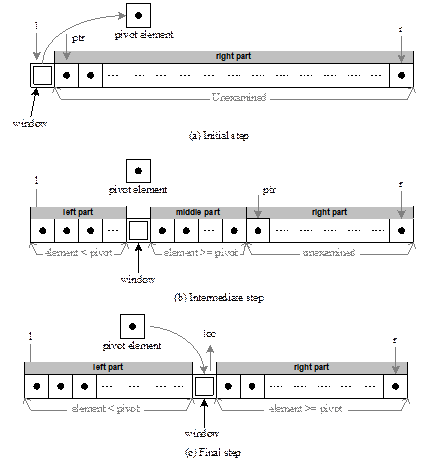
Fig. 14.43 Illustration of
Lomuto’s partition method.
Algorithm LomutoPartition
Input: A list of elements stored in an array A[l….r], where l and r are the left most and right most
indices of the list.
Output: loc,
the final location of the pivot element.
Steps:
|
1. |
pivot = A[l]
// The first
element is selected as the pivot |
||
|
2. |
window = l
// Initially the window is at
the beginning of the list |
||
|
3. |
prt = l +1 // Pointer to the first element is the sub
list of unexamined element |
||
|
4. |
While (ptr
≤ r ) do |
||
|
5. |
|
If (A[ptr]
< pivot) then
// Move smaller element to the window |
|
|
6. |
|
|
A[window] = A[ptr] |
|
7. |
|
|
A[ptr] = A[window +1] // Move larger element to
shift the window at right |
|
8. |
|
|
ptr = ptr +1
// Move ptr to the next unexamined |
|
9. |
|
Else |
|
|
10. |
|
|
ptr = ptr + 1
// Move ptr to the next
unexamined |
|
11. |
|
EndIf |
|
|
12. |
EndWhile |
||
|
13. |
A[window]
= pivot
// Place pivot to its final position |
||
|
14. |
loc = window
// Final location of the pivot |
||
|
15. |
Return(loc) |
||
|
16. |
Stop |
||
In this section, we have discussed the basic concepts
in the quick sort method and few important variations of it. In fact, a number
of variants of the quick sort method have been published. Interested readers
are advised to read the papers of Robert Sedgewick in the Communication of CAM,
Vol. 21, pages 847-857, 1978 and the paper published by J. L. Bentley and M. D.
McIcroy in Software Practice & Experience, Vol. 23, pages 1249-1265, 1993.
SORTING BY
DISTRIBUTION
In
this section, we are going to learn an interesting class of sorting algorithms.
These sorting algorithms are radically different than the previously discussed
sorting algorithms. The key features, which make these sorting algorithms distinguished
from others are:
- Sorting without key
comparison
- Running time
complexity is O(n)
In
other words, in this type of sorting algorithms, sorting operation is carried
out by means of distribution based on the constituent components in the elements.
This is why a sorting method in this class is called sorting by distribution. We shall discuss three different sorting techniques
in this class which are
·
Radix sort
·
Bucket sort
·
Counting sort
These sorting techniques are
discussed in the following sub sections.
Radix Sort
A
sorting technique which is based on radix
or base of constituent elements in
keys is called radix sort. The radixes and bases in few important number
systems are listed in Table 104.22.
Table 14.22 Radixes in few number
systems.
|
Number
system |
Radix |
Base
|
Example |
|
Binary |
0 and 1 |
2 |
0100, 1101, 1111 |
|
Decimal |
0,1,2,3,4,5,6,7,8,9 |
10 |
326,12345,1508 |
|
Alphabetic |
a, b,….,z A, B,….,Z |
26 |
Ananya, McGraw |
|
Alphanumeric |
A,…z, A….Z and 0…9 |
36 |
06IT6014 05CS5201 |
Basic principle of radix sort came from the primitive
sorting method used in the card sorting
machine. In the early computing era, such a machine used punch cards, which
are organized into 80 columns and 12 rows. In each column a hole can be punched
in one of 12 places. From decimal digits, only 10 places are used in each
column. The other 2 places are used for encoding non-numeric characteristics. A
digit key would then occupy a field of columns. For an example, suppose n numbers were to be sorted. n such numbers were then punched on n cards. Prior to sorting, all punched
cards were placed on an input deck of cards. The card-sorter looked at only one
column at a time, say list significant digit first. The cards were then
combined into the desk with the cards of least significant digit 0 preceding
the cards of least significant digit 1, preceding the cards of least
significant digit 2 and so on. Next, the entire deck was sorted in the similar
manner except this time looking at the second least significant digits. This
process continued for d times (d being the number of constituent
elements in numbers) until all cards with the most significant digit were
sorted. After the end of d passes,
all n cards were sorted.
Motivated with the mechanism of
card sorting machine, P. Hildebrandt, H. Isbitz, H. Rising and J. Schwartz
proposed the idea of radix sorting in the Journal of ACM, Vol. 6, pp. 156-163,
1959. Note that radix sort came three years earlier than the quick sort method
proposed by D. A. Hoare [Computer Journal, Vol. 5, No. 1, pp. 10-15, 1962].
Hildebrandt et al. followed the principle of radix to sort binary numbers in
computer and is illustrated in Figure 10.45. In Figure 10.45 10 numbers in
binary system each of 4 bits are sorted with scanning from top to bottom. It
can be noted that 4 passes are required to sort 4-bits binary numbers.
Now, let us formulate an algorithm for radix sort. Let
us consider a number system with base b,
that is, the constituent element in any key value ranges between 0, 1, 2,…..,(b-1). Further, assume that number of
components in a key value is c and n number of key values is there in the
input list. The output list will be in the ascending order of the key values.
In other words, let n key values are
stored in an array A[1, 2…, n] and any key ![]() = ai1 ai2…aic where
= ai1 ai2…aic where ![]() for all
for all ![]() .
.

Fig. 14.45 Principle of the radix sort.
In the radix sort method, other than the input array,
we will need b auxiliary queues. Let
the queues be Q0[1…n], Q1[1…n], …, Qb-1[1…n]. Note that maximum size of each queue is n, which is the number of key values in
the input list. With this preliminary, we define the algorithm radix sort which
is stated below.
Algorithm RadixSort
Input: An array A[1,
2, ..., n], where n is the number of elements.
Output: n elements are arranged in A in ascending order.
Remark: b
number of auxiliary arrays each of size n
is used.
Steps:
|
|
/* For each base in the number system */ |
|||
|
1. |
For i =1 to c do //
c denotes the most significant position |
|||
|
2. |
|
For j =1 to n do
// For all elements in the array A |
||
|
3. |
|
|
x = Extract(A[j], i) // Get the i-th component in the j-th element |
|
|
4. |
|
|
Enque(Qx, A[j]) |
|
|
5. |
|
EndFor |
||
|
|
|
/* Combine all elements from all auxiliary arrays to A (assume A is empty*/ |
||
|
6. |
|
For k = 0 to (b-1) do |
||
|
7. |
|
|
While Qk is not empty do |
|
|
8. |
|
|
|
y = Dequeue(Qk)
// Dequeue of y from the queue Qk |
|
9. |
|
|
|
Insert(A,
y)
// Insert y into A |
|
10. |
|
|
EndWhile |
|
|
11. |
|
EndFor |
||
|
12. |
EndFor |
|||
|
13. |
Stop |
|||
Illustration of the algorithm RadixSort
The
outermost loop (Step 1- Step 12) in the algorithm RadixSort iterates c
number of times. In each iteration, it distributes n elements into b number
of queues. This is done through an inner
iteration (Step 2 - Step 5). Next, starting from the queue Q0 to Q b-1
all elements are dequeued one by one and inserted into the array A. This is done in another inner loop,
namely, Step 6-11. When the outermost loop (step 1-12) completes its all runs,
elements appear in the array A in
ascending order. In the above mentioned
algorithm, we assume the procedure Enque(Q, x)
to enter an element x into an array Q in FIFO (queue order) and y = Dequeue(Q) the procedure to delete an element
from Q in FIFO order. Another procedure
Extract(A, i) returns the i-th component in the element A.
The algorithm RadixSort
is illustrated in Fig. 14.46 with 10 numbers in decimal system and each number
is of 3 digits. There are 3 passes in the algorithm. The different tasks in the
first pass is shown in Figure 14.46(a) to Figure 14.46(c). An input list
containing 10 numbers each of three digits is shown in Figure 14.44(a). Result
of the execution of the inner loop in Step 2- 5 is shown in Figure 14.46(b).
The result of combining the distribution according to another inner loop in
Step 6-11 is shown in Figure 10.46(c). This ends the first pass. It can be
noted that all elements are arranged in the array A according to the ascending order of their least significant
digits. The arrangement of elements in the array A as obtained in the first pass becomes the input list to the
second pass. Distribution of elements and combining there after in the second
pass are shown in Figure 14.46(d) and Figure 14.46(e), respectively. At the end
of the second pass all elements in the array A are arranged in ascending order with respect to their last two
digits. Result of the third pass is shown in Figure 14.46(f) and Figure 14.46(g).
Finally the list appears as sorted in ascending order.
Note: The algorithm radix sort as stated above is a general version and
applicable to any number system. For the binary number system we should take c = 2, b = 0, 1 and the sorting algorithm particular to this system is
termed as bin sort. The radix sort is
touted as digit sort when it sorts
numbers represented in decimal number system, where c = 10, b = 0, 1, …, 8,
9. A special case of radix sort is for alphabetic system (that is, a string of
characters) when c = 26, b = a,
b, …, y, z, A, B,
… Y, Z and the radix sort in this special case is termed as lexicographic sort.


Fig 14.46 Continued.

Fig 14.46 Illustration of the
RadixSort algorithm.
Analysis of the algorithm RadixSort
At
the beginning of this section, we mentioned that the radix sort is a sorting
method, which does not involve any key comparison. Further, it was also
mentioned that the run time complexity of the radix sort algorithm is O(n).
The run time of the radix sort algorithm is mainly due to two operations:
distribution of key elements and followed by a combination. It can be easily
checked that the run time remains invariant irrespective of the order of the
elements in the list. So, we discuss a general treatment to calculate the time
requirement in the radix sort algorithm.
Time requirement
Let, a
= time to extract a component from an element.
e
= time to enqueue an element in an array.
d
= time to dequeue an element from an array.
Time
for distribution operation = (a+e)n [in Step 2-5]
Time
for combination = (d+e)n [in Step 6-12]
Since
these two operations are iterated c
times (Step 1-12), the total time of computations is given by
![]()
= ![]()
Since, a, d, e, and c all are constants for a number
system, we have ![]() .
.
Storage space requirement
It
is evident that radix sort is not an
in place sorting method. It requires b auxiliary arrays to maintain b queues, where b denotes the base of the number system. The size of each array is n, so that in worst case it can
accommodate all n elements. Thus, the
total storage space required in radix sort is
![]()
Thus,
![]() , b being a
constant.
, b being a
constant.
From the analysis of the algorithm RadixSort, we can summarize the results,
which are shown in Table 14.23. It can be noted that different arrangements of
elements in an input list do not bear any significance in the radix sort.
Table 14.23 Analysis of the algorithm RadixSort.
|
Memory |
Time |
Remark |
|
|
|
Here, b denotes the base of
the number system and a, c, d, and e are constants |
Table 14.24 shows the run time complexity of the
algorithm RadixSort.
Table 14.24 Storage and Time complexities of the algorithm
RadixSort.
|
Complexity for |
Complexity |
Remark |
|
Memory |
|
Irrespective of
arrangements of elememts. |
|
Time |
|
Bucket Sort
Radix
sort is efficient for a list of small size and when the size of keys is not too
large. Further, radix sort demands huge memory as auxiliary memory. For
example, if the radix is a digit sort then
it requires 10 times extra storage space than the size of the list. This is why
we can not afford lexicographic sort in a memory constrained application in
spite of its O(n) running time complexity. To overcome this
problem, an alternative version of distribution sort term as bucket sort has
been proposed by E. J. Isaac and R. C. Singleton in Journal of ACM, Vol-3, pp.
169-174, 1956. We discuss the idea of bucket sort to sort elements in decimal
number system. The basic idea of the bucket sort in this case is to use 10
numbers of buckets. Suppose we want to sort a list of n numbers. The bucket sort comprises the following steps.
1. Distribution of n
elements among 10 buckets (in general 10 << n).
2. Sort each bucket individually.
3. Combine all buckets to get the output list.
Let us explain all these steps in details.
Distribution of n
elements among 10 buckets
Since
the basic objective of the bucket sort is to reduce the memory requirement, m buckets are maintained using a hash
table of size m (for hash table, see
Chapter 6, Section 6.4 of this book). Following a suitable hashing techniques and chaining
technique, an element will be placed in a bucket. In other words, hashing
calculates the address of an element and it is placed into that address in a
chained manner (because, zero or more elements may be there in a bucket). This
is why, the bucket sort is also alternatively termed as address calculation sort. Note that, chaining uses dynamic storage
structure (such as, single linked list) and hence number of nodes in all
buckets is same as the input size. Let us illustrate the distribution of
elements among the bucket with an example. Suppose a list of 12 elements stored
in an array A as shown in Figure 14.47(a)
are to be sorted in ascending order. Let the hash method h(k) returns the most
significant digit in the key value k.
The distribution of all elements in A
among the 10 buckets, which are pointed by hash table H is shown in Figure 14.47(b).
Sorting the Buckets
Any
sorting method then can be applied to sort each bucket separately. The best
choice is to use straight insertion sort. The implementation of straight
insertion sort in this case is straight forward. In fact, this can be done
during the distribution step itself. In other words, elements can be inserted
to buckets in sorted fashion, that is, in ascending order of key values. The
buckets after insertion sort are shown in Figure 14.47(c).
Combining
the buckets
The
buckets so obtained in the previous step can be combined to obtain the list of
sorted elements. Following the link in the hash table, each bucket can be
traversed sequentially. While visiting a node in a bucket, the key value in the
node will be placed into the output list (see Figure 14.47(d)).

Fig. 14.47 Continued.
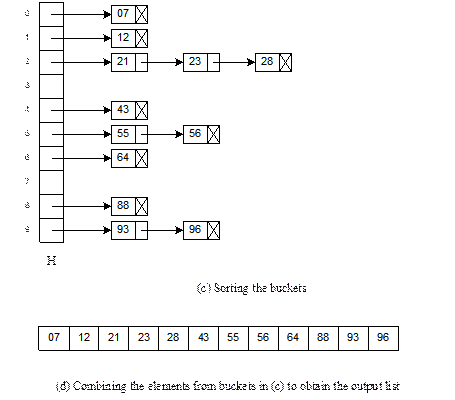
Fig. 14.47 Illustration of the
bucket sort.
The
bucket sorting technique as discussed above is formulated through the algorithm
BucketSort.
Algorithm BucketSort
Input: An array A[1,
2, ..., n] of n elements.
Output: n elements are arranged in A in ascending order
Remark: A hash table H stores pointers to 10 buckets; buckets are maintained using
single linked
list structure.
Steps:
|
|
/* Distribution of input elements into buckets */ |
||||
|
1. |
For i =1 to n do |
||||
|
2. |
|
k = A[i] |
|||
|
3. |
|
x = GetMSB(k) // The
hash function returning the most significant // digit as the address to the hash table |
|||
|
4. |
|
ptrToBucket = H[x] // Point to the bucket where k has to be
inserted |
|||
|
|
|
/* Insert the element into bucket */ |
|||
|
5. |
|
ptr1 = ptrToBucket |
|||
|
6. |
|
ptr = GetNode()
// Allocate memory for a new node |
|||
|
7. |
|
ptr→data = k |
|||
|
8. |
|
If (ptr1 =
NULL) then
// If the bucket is empty |
|||
|
9. |
|
|
H[x] = ptr |
||
|
10. |
|
|
ptr→link = NULL |
||
|
11. |
|
Else
// Find the place in the bucket |
|||
|
12. |
|
|
While
(ptr1 ≠ NULL) do |
||
|
13. |
|
|
|
If (k
≥ ptr1→data) then |
|
|
14. |
|
|
|
|
ptrToBucket = ptr1 |
|
15. |
|
|
|
|
ptr1 = ptr→link |
|
16. |
|
|
|
Else |
|
|
17. |
|
|
|
|
Break()
// Quit the loop |
|
18. |
|
|
|
EndIf |
|
|
19. |
|
|
EndWhile |
||
|
20. |
|
|
ptrToBucket →link =
ptr
// Insert here |
||
|
21. |
|
|
ptr→link = ptr1 |
||
|
22. |
|
EndIf |
|||
|
23. |
EndFor |
||||
|
|
/* Combine buckets into the array A */ |
||||
|
24. |
j =1 |
||||
|
25. |
For i = 0
to 9 do
// Traverse each bucket |
||||
|
26. |
|
ptrToBucket = H[i]
// Point to the i-th bucket |
|||
|
27. |
|
While
(PtrToBucket ≠ NULL) do // Visit all
nodes in the current bucket |
|||
|
28. |
|
|
A[j] =
ptrToBucket→data //
Place the element in the list |
||
|
29. |
|
|
j = j +1 |
||
|
30. |
|
|
ptrToBucket =
ptrToBucket→link
// Move to the next |
||
|
31. |
|
EndWhile |
|||
|
32. |
EndFor |
||||
|
33. |
Stop |
||||
Analysis of the algorithm BucketSort
Memory Requirement
In
the BucketSort algorithm, following amount of storage spaces is needed.
To maintain the hash table = 10
Number of node in the bucket = n
Therefore,
the total storage space (Sn) required is
S(n) = n + 10
Hence,
the storage complexity in the BucketSort
algorithm is
S(n) = O(n)
Run time requirement
To
analyze the running time in the algorithm BucketSort,
we are to calculate the time to distribute n
number of input elements into 10 buckets (in Step 1-23) and thereafter
combining elements in buckets to output list (in Step 24-32). It can be
observed that the loop (Step 1-23) executes n
times to distribute n elements among
10 buckets. In each iteration, it inserts an element into a bucket in a manner
of straight insertion sort (See Section 10.3.1). That is, each bucket is built
up with the straight insertion sort and hence the run time for this task is
mainly governed by the time to build all buckets. We know that the algorithm StraightInsertionSort runs in quadratic
time, that is, in![]() . The running time T(n) of the bucket sort then can be
written as
. The running time T(n) of the bucket sort then can be
written as
T(n) = ![]()
The
first term calculates the run time to distribute n elements into 10 buckets so that each bucket is in sorted
order. In the expression, ni denotes the number of
elements in the i-th bucket. It may
be noted that number of elements in a bucket varies from 0 (minimum) to n (maximum). Hence, the value of ni in the above expression
varies between 0 to n. The second
term counts the time for combine operation in Steps 24-30. It can be find that
T(n) = ![]()
= ![]() where k > 0 is a constant.
where k > 0 is a constant.
This signifies an important result that although
bucket sort employs straight insertion sort having quadratic time (![]() ) complexity, the average run time of the bucket sort turns
to be a sorting algorithm with linear time (
) complexity, the average run time of the bucket sort turns
to be a sorting algorithm with linear time (![]() ) complexity.
) complexity.
Note:
i.
It can be
observed that if the input list is such that in all passes of the execution of the BucketSort, elements are “Balanced” way distributed among the
buckets, that is, all buckets contains nearly equal number of elements then it
runs faster. On the other hand, if all elements cluster into a single bucket
then it runs worst (eventually, same as the insertion sort).
ii. The BucketSort is
not truly a sorting algorithm without any key comparisons, because key
comparisons are possibly involved while elements are placed in a bucket.
Moreover, it also employs insertion sort.
From the analysis of the algorithm BucketSort, we can summarize the results
as shown in the Table 14.25. Like in RadixSort,
in the BucketSort also different
ordering of elements in an input list is not significant.
Table 14.25 Analysis of the algorithm BucketSort.
|
Memory |
Time |
Remark |
|
|
|
Here, c and k are some
positive constants |
Table 14.27 shows the storage
and run time complexity of the algorithm BucketSort.
Table 14.27 Storage and time complexities of the algorithm
BucketSort.
|
Complexity
for |
Complexity |
Remark |
|
Memory |
|
For large values of |
|
Time |
|
SORTING BY MERGING
A
class of sorting algorithms based on the principle of “merging” or “collating”
is discussed in this section. Suppose, A
and B are two lists with n1 and n2 elements, respectively. Also assume that both the
lists are arranged in ascending order. Merging is an operation that combines
the elements of A and B into another list C with n = n1+n2 elements in it and elements in C are also in ascending order. Sorting scheme based on this merging
operation is called sorting by merging and is important for the following two
reasons.
1. The principle is easily
amenable to divide and conquer technique.
2. Suitable for sorting very
large list, even the entire list is not necessarily to be residing
in main memory.
In
sorting by merging technique, the merging operation plays important role. In
the following section, we discuss this operation.
Simple Merging
In
fact, a large number of merging techniques are known. In this section, we
discuss the simple most of them. Let us discuss the simple merging operation
with an example. Merging operation with two lists A and B is shown in Figure
10.52. The list after merge is sorted into another list C. Initially, the list C
is empty. i, j and k are the pointers
pointing to some elements in list A, B and C, respectively. In other words, A[i] refers to the i-th element in the list A etc. Initially they point to first
element in each list (see Figure 10.52(a)).
The merge operation is a repetition of compare and
move operations. In each repetition we compare A[i] and B[j] and smaller of A[i] and B[j]
is moved to C[k]; if A[i] is moved to C[k] then pointer i is moved one step to right, otherwise
the pointer j. After such a move, the
pointer k is moved to the next
location in the list C. This is shown
in Figure 10.52(b). These steps continue until either the list A or list B is empty. Next, if A is
empty then the remaining element from the list B are moved to the list C.
Otherwise, if B is empty then the
remaining elements from the list A
are moved to the list C. Figure
10.52(c) shows the tailing part of the list B
is moved to C when A is scanned to an end.
The above stated merge operation
can be defined iteratively or recursively. Both descriptions are mentioned
below.
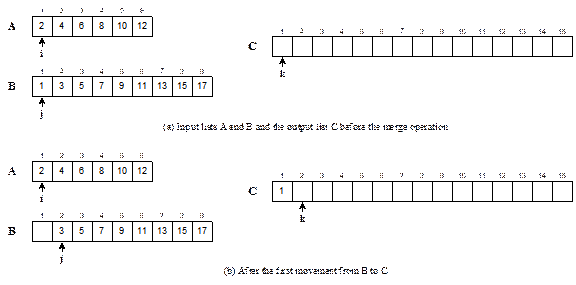
Fig. 14.52 Continued.

Fig. 14.52 Illustration of the
merge operation.
Algorithm SimpleMerge_Iterative //
Iterative
definition of merge operation
Input: Two list A
and B of size n1 and n2,
respectively. Elements in both the list A and B are sorted in ascending order.
Output: An output list with n elements sorted in ascending order, where n = n1 + n2
Steps:
|
1. |
i
= 1, j = 1, k = 1
// Three pointers, initially point to first locations |
|||
|
2. |
While(i ≤ n1 and j ≤ n2)
do |
|||
|
3. |
|
If (A[i] ≤ B[j]) then |
||
|
4. |
|
|
C[k] = A[i] |
|
|
5. |
|
|
i = i+1, k = k+1 |
|
|
6. |
|
Else // A[i] > B[j] |
||
|
7. |
|
|
C[k] = B[j] |
|
|
8. |
|
|
j
= j+1, k = k+1 |
|
|
9. |
|
EndIf |
||
|
10. |
EndWhile |
|||
|
11. |
If (i > n1) then
//
A is fully covered |
|||
|
12. |
|
For p = j to n2 do
// Move the rest of the elements in B to C |
||
|
13. |
|
|
C[k] = B[p] |
|
|
14. |
|
|
p = p+1, k = k+1 |
|
|
15. |
|
EndFor |
||
|
16. |
Else |
|||
|
17. |
|
If (j > n2 ) then
// B is fully covered |
||
|
18. |
|
|
For p = i to n1 do |
|
|
19. |
|
|
|
C[k]
= A[l]
// Move the rest of the elements in A to C |
|
20. |
|
|
|
p
= p + 1, k = k + 1 |
|
21. |
|
|
EndFor |
|
|
22. |
|
EndIf |
||
|
23. |
EndIf |
|||
|
24. |
Stop |
|||
Algorithm SimpleMerge_Recursive // The recursive
definition of merge operation
Input: A and B are two lists
with i and j are the two pointers pointing some locations, respectively.
Output: Elements after merging is sorted in C.
Remark: n1
and n2 are the size of the
list A and B, respectively. k is a
current pointer at C. n1
and n2 are two constants
and k is the global variable to the
recursive calls. A, B and C are the globally declared
lists.
Steps:
|
1. |
If (i > n1) then
// Termination condition check: If A is fully |
||
|
2. |
|
For p = j to n2 do
// Move
the rest of the elements in B to C |
|
|
3. |
|
|
C[k] = B[j] |
|
4. |
|
|
p = p +1, k = k+1 |
|
5. |
|
EndFor |
|
|
6. |
Return |
||
|
7. |
EndIf |
||
|
8. |
If (j > n2) then
// Termination condition check: If B is fully covered |
||
|
9. |
|
For p = i to n1 do
// Move the rest of the elements in A to C |
|
|
10. |
|
|
C[k] = A[i] |
|
11. |
|
|
p = p +1, k = k+1 |
|
12. |
|
EndFor |
|
|
13. |
|
Return |
|
|
14. |
EndIf |
||
|
15. |
If (A[i] ≤ B[j]) then |
||
|
16. |
|
C[k] = A[i] //Move
the smaller from A to C |
|
|
17. |
|
k = k +1, i = i +1 |
|
|
18. |
Else
//
A[i] > B[j] |
||
|
19. |
|
C[k] = B[j] //Move
the smaller from B to C |
|
|
20. |
|
k = k +1, j = j +1 |
|
|
21. |
EndIf |
||
|
22. |
SimpleMerge_Recursive(A, B, i, j) // Recursive
call of merge |
||
|
23. |
Stop |
||
Analysis of the simple
merge operation
In
the following the time complexity and storage complexity of the merge operation
are analyzed. We analyze this with reference to the iterative definition of
algorithm. Similar procedure can be followed to analyze the recursive version
of the algorithm.
Time complexity
Suppose,
two lists A and B with n1 and n2 elements respectively.
Both n1, n2 > 0.
Let
us analyze different cases of the merge operation.
Case 1: n1 = 1 and n2 = n -1 and A contains the smallest
element
In
this case, we require only one comparison (see Figure 10.53(a)).
Case 2: n2 = 1 and n1 = n -1 and B contains the smallest
element
In
this case, we require only one comparison (see Figure 10.53(a)).
Case 3: n1 = 1 and n2 = n -1 and A contains the largest
element
In
this case, we require n-1 comparisons (see Figure. 10.53(b)).
Case 4: n2 = 1 and n1 = n -1 and A contains the largest
element
In
this case, we require n-1 comparisons
(see Figure 10.53(b)).
Case 5: Either
A or B contains a single element, which is neither smallest nor largest
In
this case, the number of comparisons is decided by the single element itself
(see Figure. 10.53(c)). Without the loss of generality, we can say that on the
average, n/2 number of comparisons is
required.
Case 6: The largest element in A is smaller than the smallest element in B and
vice-versa
In
this case (see Figure 10.53(d)), the number of comparisons in best case is min(n1,
n2), that is, the minimum of n1 and n2.
Case 7: Otherwise, that is, any trivial orderings
Such
a case is illustrated in Figure 10.53(e). In this case, we may need as many as n-1 comparisons.
From the different snapshots in Figure 10.53, we see
that in the best and worst cases, the merge operation requires 1 and (n-1) comparisons, respectively. These
two cases are corresponding to the merging of two lists, one of which is the
smallest and the other is the largest. Now, in a case when two input lists are
an arbitrary sizes, say n1
< n and n2 < n
the number of comparisons is minimum of n1
and n2, which can be taken
as on the average n/2 comparisons.
There is also another worst case situation with n-1 comparisons, where the last elements in the two lists are the
largest and next to the largest.
Now we summarize the time complexity of the algorithm
merge operation as below. Let T(n) denotes the number of comparisons to
merge two lists of sizes n1
and n2 to produce a list
of n elements.
Best
case: T(n) = min(n1,
n2)
= 1 if n1 = 1 or n2
= 1
Worst
case: T(n) = n-1
Average
case: T(n) = n/2
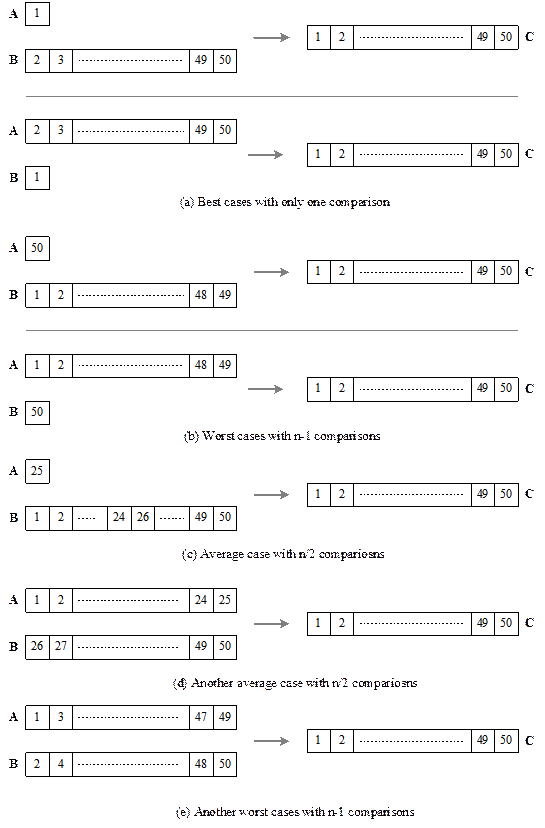
Fig. 14.53 Different situations of
the merge operation.
Space complexity
The
merge operation that we have defined assume that the output list is stored in a
separate storage space C and size of
this should be n = (n1 + n2). Hence, the storage complexity of merging n elements is
S(n) = n1+n2 = n (say)
(This is although apart from the storage spaces for
the input lists.)
Merge Sort
So
far we have discussed the merging operation. In this section, we shall discuss
the sorting by such a merging operation. All sorting method based on merging
can be divided into two broad categories:
·
Internal merge sort and
·
External merge sort
In case of internal merge sort, the lists under
sorting are small and assumed to be stored in the high speed primary memory. In
other hand, external merge sort deals with very large lists of elements such
that size of primary memory is not adequate to accommodate the entire lists in
it. We first discuss the internal merge sort techniques. External merge sort
techniques are discussed in the next sub section.
Internal Merge Sort
The
internal merge sort (here after we shall tell this as merge sort simply)
technique closely follows the divide-and-conquer paradigm. Let a list of n elements to be sorted with l and r being the position of leftmost and rightmost elements in the
list. The three tasks in this divide-and-conquer technique are stated as
follows.
Divide: Partition
the list midway, that is, at ![]() into two sub lists
with
into two sub lists
with ![]() elements in each, if n
is even or
elements in each, if n
is even or ![]() and
and ![]() elements if n is
odd.
elements if n is
odd.
Conquer: Sort the two lists recursively using the merge sort.
Combine:
Merge the sorted sub lists to obtain the sorted output.
The divide-and-conquer strategy used in the merge sort
is illustrated with a schematic diagram as shown in Fig. 10.56.

Fig. 14.56 Divide-and-conquer
strategy in the internal merge sort.
In the divide-and-conquer strategy, the task divide merely calculates the middle
index of the list. The conquer step is to solve the same problem but for two
smaller lists. It can be done recursively and the recursion should terminate
when the list to be sorted has length 1, in which case there is no work to be
done, since every list of length 1 is already in sorted order. The third step
namely combine does the merging. We assume that this merging operation does not
require any auxiliary list to store the output list; rather it merges two
adjacent sub arrays and putting the resulting merged array back into the same
storage space originally occupied by the elements being merged. Merge sort
based on the divide-and-conquer strategy is illustrated with an example to sort
a list of 6 elements as shown in Figure 14.57. Figure 14.57 shows the
recurrence tree implying the order different tasks are executed.
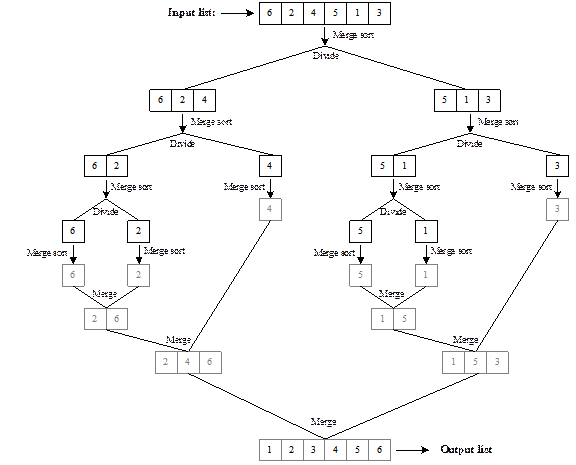
Fig. 14.57 Illustration of the
merge sort.
Now
we make a precise definition of the merge sort technique through detail
procedure below.
Algorithm MergeSort
Input:
An array A[l…r] where l and r are the lower and upper indexes of A.
Output: Array A[l…r] with all elements are arranged in ascending order.
Steps:
|
1. |
If (r |
|
|
2. |
|
Return
// Termination of recursion |
|
3. |
Else |
|
|
4. |
|
|
|
5. |
|
MergeSort(A[l…mid])
// Conquer for the left-part |
|
6. |
|
MergeSort(A[mid+1…r])
// Conquer for the right-part |
|
7. |
|
Merge(A, l, mid, r) //
Combine: Merging the sorted left- and right- parts |
|
8. |
EndIf |
|
|
9. |
Stop |
|
The algorithm MergeSort
is defined recursively. Step1 is the termination condition of the recursive
procedure. In Step 4, we compute the middle index of the input array A and hence the task divide is
accomplished. In step 5 and 6 the recursive calls of merge sort procedure on
two sub arrays. These two steps comprise the conquer tasks. In Step 7, the merge
operation of two sorted sub arrays (as resulted in the Steps 5 and 6) takes
place, which finally produces the sorted output. This is corresponding to the
task combine.
The merge operation as referred
in Step 7 can be obtained by slightly refining the algorithm as stated in
previous section.. Further, we modify the iterative version of the simple merge
operation so that the new version works on two lists but in the same array.
This is stated as algorithm Merge
below.
Algorithm Merge
Input: An array A with two sub arrays where indexes ranges from l to mid
and mid+1 to r.
Output: The two sub
arrays are merged and sorted in the array A.
Remark: Assume extra storage space of C having size |r-l+1| to store the entire array A.
Steps:
|
1. |
i
= l, j = mid+1, k = 1 // i and j points at the
beginning of the two sub arrays and k
to C |
|||
|
2. |
While ((i≤mid) and
(j≤r)) do |
|||
|
3. |
|
If (A[i] ≤ A[j] ) then |
||
|
4. |
|
|
C[k]
=A[i] |
|
|
5. |
|
|
i
= i+1, k = k+1 |
|
|
6. |
|
Else //
A[j] ≤ A[i] |
||
|
7. |
|
|
C[k]
= A[j] |
|
|
8. |
|
|
j
= j+1, k = k+1 |
|
|
9. |
|
EndIf |
||
|
10. |
EndWhile |
|||
|
11. |
If (i>mid) and (j≤r) then
// Copy rest of the right sub array to C |
|||
|
12. |
|
For m = j to r do |
||
|
13. |
|
|
C[k]
= A[m] |
|
|
14. |
|
|
M = m+1, k = k+1 |
|
|
15. |
|
EndFor |
||
|
16. |
Else |
|||
|
17. |
|
If (i≤mid) and (j>r) then
// Copy rest of the left sub array to C |
||
|
18. |
|
|
For m = i to mid do |
|
|
19. |
|
|
|
C[k]
= A[m] |
|
20. |
|
|
|
m
= m+1, k = k+1 |
|
21. |
|
|
EndFor |
|
|
22. |
|
EndIf |
||
|
23. |
EndIf |
|||
|
24. |
For m = 1 to k-1 do
// Copy C to A |
|||
|
25. |
|
A[l+1] = c[m] |
||
|
26. |
|
m
= m+1 |
||
|
27. |
EndFor |
|||
|
28. |
Stop |
|||
It may be noted that the algorithm Merge is same as
the previously defined algorithm SimpleMerge_Iterative.
However, in the later version, we use two lists in the same array and copy the
output list to the input array.
Analysis of the merge
sort
Now
it is the turn to analyze the complexity of the algorithm MergeSort.
Time complexity
The basic operation in the merge sort is the
key comparison. It is evident that merge sort on just one element requires only
one comparison. Let c1 be
the time for this. When n>1, we
break down the running time for the 3 tasks involved in the merge sort
procedure. Let T(n) denotes the time to sort n
elements. We can express the T(n) as
below.
T(n) = c1 if n = 1
=
![]() if n > 1
if n > 1
Here,
D(n)
denotes the time for divide task. The divide step just computes the middle of
the sub array, which takes constant time. Thus let D(n) = c2. Next, each divide step
yields two sub arrays of sizes ![]() and
and![]() . Since, we recursively solve two sub problems, the running
time for this task is
. Since, we recursively solve two sub problems, the running
time for this task is ![]() . Finally, the third task, namely, combine where the
algorithm MergeSort merges two lists
to an output list of size n. Let C(n)
denotes the time to merge two lists of sizes
. Finally, the third task, namely, combine where the
algorithm MergeSort merges two lists
to an output list of size n. Let C(n)
denotes the time to merge two lists of sizes
![]() and
and ![]() so that the output
list is of size n.
so that the output
list is of size n.
In order to simplify the calculation, we consider the
following assumptions.
1. Number of elements in the list is a power of 2. let n = 2k (with this assumption, therefore, each
divide step yields two sub sequences of size exactly n/2). Thus ![]()
2. We consider the merge operation whose, worst case time
complexity is C(n) = n-1
With these assumptions, we express the recurrence
relation in Equation (1) as follows.
![]() if n = 1
if n = 1
= ![]() if n > 1
if n > 1
Let
us solve the recurrence relation in Equation (10.47b) as proceed below.
![]()
![]()
= ![]() [Expanding
[Expanding![]() ]
]
= ![]() [After the
first expansion]
[After the
first expansion]
= ![]() [Expanding
[Expanding![]() ]
]
= ![]() [After the
second expansion]
[After the
second expansion]
… … … … … …
[After the (k-1) expansions]
= ![]()
= ![]()
= ![]()
= ![]()
Since,
n = 2k and T(1) = c1, finally, we get
T(n) = ![]()
Equation
10.48 gives the time complexity of the algorithm in worst case.
Best case time complexity
The
best case occurs when the list to be sorted is almost sorted in order. In such
a situation, the merge operation requires n/2
operations and time complexity can be obtained as
![]()
Average case time complexity
A
detailed calculation on the average case analysis reveals that, on the average,
the time complexity of merge sort is
![]()
Space complexity
The
algorithm we have discussed use the merge operation, which stores the output
list into an auxiliary storage space. The storage space in merge operation is =
n (when we merge two sub lists of
size n/2 elements in each). Hence we
need extra storage space n other than
the input list it self. Therefore, the storage complexity to sort n elements is
S(n) = n
Comparison of quick
sort and merge sort
We
have learned that quick sort and merge sort are both the sorting techniques
based on divide-and-conquer strategy. They differ in the ways they divide the
problems and later combine the situations. Quick sort is characterized as “hard division, easy combination” while
merge sort is characterized as “easy
division, hard combination”. For quick sort the work horse is partition in
the divide step of the divide-and-conquer framework; hence combine step does
nothing. For merge sort the work horse is merge in the combine step; the divide
step in this framework does one simple calculation only. Apart from the
bookkeeping operations associated in each sorting method the performance of a
sorting method is really judged by the “hard”
section. In other words, the operations those are involved in these “hard”
sections decides the performance of sorting methods. So, better performance of
these operations yields better performances.
Although both partition and
merge operations in worst case has time complexity Θ(n) [note that number of comparisons in partition is n-1 and number of comparisons in merge
is (n-1)] but the overall complexity
so greatly influenced by how it is divide problems into sub-problems. Both the
algorithms divide the problem into two sub problems; however, with merge sort, the
two sub problems are of almost equal size always. Whereas with quick sort an
equal sub division is not guaranteed. This difference between the two sorting
methods appears as the deciding factor of their run time performances.
So far storage space requirement
is concerned quick sort is more preferable than the merge sort because the
merge sort has extra overhead of O(n),
which is not required in the quick sort (however, it requires space for stack,
which is usually less compared to the size of the input list). In a nutshell,
if memory is not a constraint then merge sort is a better choice than the quick
sort.